Гомотетия
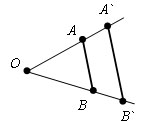
Пусть есть некая фигура F и фиксированная точка O. Проведем через произвольную точку A фигуры F полупрямую OA и отложим на ней отрезок OA` = k*OA, k>0. Преобразование фигуры F, при котором любая ее точка A переходит в точку A`, построенную данным способом называется гомотетией относительно точки O. Число k – коэффициент гомотетии.
Гомотетия. Свойство
Теорема
Гомотетия есть преобразование подобия.
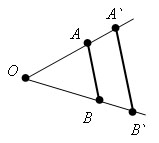
Доказательство.
Пусть O – центр гомотетии, k – коэффициент гомотетии, A и B – две произвольные точки фигуры.
При гомотетии точки A и B переходят в точки A` и B` на лучах OA и OB соответственно, причем OA`=k*OA, OB`=k*OB. Следовательно
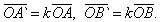
Тогда вычитая равенства почленно, получим:
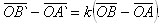
Так как
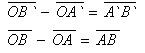
То
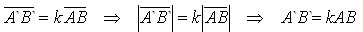
Следовательно, гомотетия есть преобразование подобия. Теорема доказана.
Подобие фигур
Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия.
Теорема
Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигуры F1 и F3 подобны.
Доказательство.
Пусть точки X1 и Y1 – две произвольные точки фигуры F1. При преобразовании подобия, фигура F1 переходит в фигуру F2, при этом точки X1 и Y1 переходят в X2 и Y2 так, что X2Y2 = k1*X1Y1
Соответственно преобразование подобия переводит фигуру F2 в F3 и X3Y3 = k2*X2Y2.
Следовательно, X3Y3 = k2*X2Y2=k2*k1*X1Y1.
Как видно, что преобразование фигуры F1 в F3, получающееся при последовательном выполнении двух преобразовани2 подобия, есть подобие. Значит фигуры F1 и F3 подобны. Теорема доказана.
Признак подобия треугольников по двум углам
Теорема
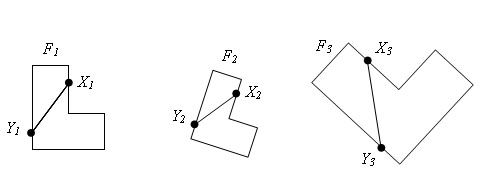
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство.
Пусть у треугольников ABC и A1B1C1 ∠ CAB = ∠ C1A1B1, ∠ ABC = ∠ A1B1C1. Докажем, что Δ ABC подобен Δ A1B1C1.
Пусть k = AB/A1B1. Подвергнем Δ A1B1C1 гомотетии с коэффициентом k. Получится некоторый Δ A2B2C2.
Δ A2B2C2 = Δ ABC по второму признаку равенства треугольников (∠ C2A2B2 = ∠ C1A1B1 = ∠ CAB, ∠ A2B2C2 = ∠ A1B1C1 = ∠ ABC так как преобразование подобия сохраняет углы, A2B2 = k*A1B1 = AB, по условию).
Треугольники A1B1C1 и A2B2C2 гомотетичны, следовательно подобны. Δ A2B2C2 = Δ ABC, следовательно подобны тоже, а значит треугольники A1B1C1 и ABC подобны. Теорема доказана.
Признак подобия треугольников по двум сторонам и углы между ними
Теорема
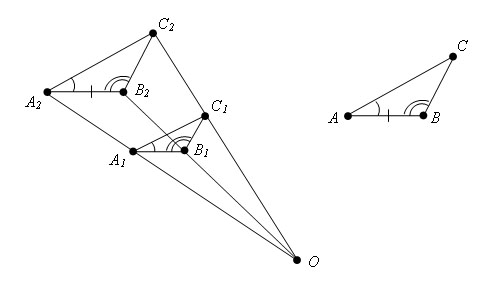
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
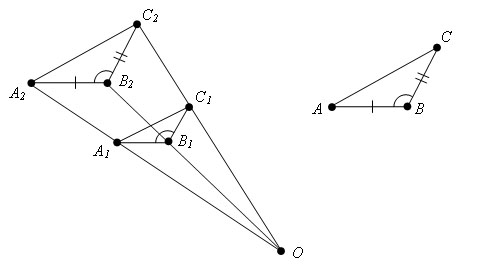
Доказательство.
Пусть у треугольников ABC и A1B1C1 ∠ CBA = ∠ C1B1A1, AB = k*A1B1, BC = k*B1C1. Докажем, что Δ ABC подобен Δ A1B1C1.
Подвергнем Δ A1B1C1 гомотетии с коэффициентом k. Получится некоторый Δ A2B2C2.
Δ A2B2C2 = Δ ABC по первому признаку равенства треугольников (∠ A2B2C2 = ∠ A1B1C1 = ∠ ABC так как преобразование подобия сохраняет углы, A2B2 = k*A1B1 = AB, B2С2 = k*B1С1 = BС, по условию).
Треугольники A1B1C1 и A2B2C2 гомотетичны, следовательно подобны. Δ A2B2C2 = Δ ABC, следовательно подобны тоже, а значит треугольники A1B1C1 и ABC подобны. Теорема доказана.
Признак подобия треугольников по трем сторонам
Теорема
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
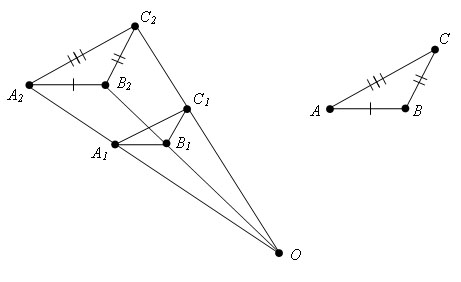
Доказательство.
Пусть у треугольников ABC и A1B1C1 ∠ CBA = ∠ C1B1A1, AB = k*A1B1, BC = k*B1C1, AC = k*A1C1. Докажем, что Δ ABC подобен Δ A1B1C1.
Подвергнем Δ A1B1C1 гомотетии с коэффициентом k. Получится некоторый Δ A2B2C2.
Δ A2B2C2 = Δ ABC по третьему признаку равенства треугольников (A2С2 = k*A1С1 = AС, A2B2 = k*A1B1 = AB, B2С2 = k*B1С1 = BС, по условию).
Треугольники A1B1C1 и A2B2C2 гомотетичны, следовательно подобны. Δ A2B2C2 = Δ ABC, следовательно подобны тоже, а значит треугольники A1B1C1 и ABC подобны. Теорема доказана.
Углы, вписанные в окружность
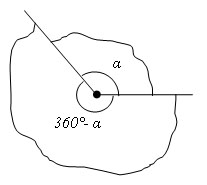
Плоскость разбивается углом на две части, на два плоских угла. Плоские углы с общими сторонами называются дополнительными . Мерой плоского угла, являющегося частью полуплоскости, называется градусная мера угла с теми же сторонами. Мерой плоского угла, содержащего полуплоскость, называется величина 360° – α, где α – градусная мера дополнительного плоского угла.
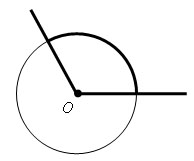
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
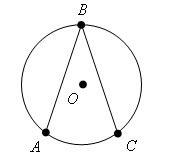
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность. ∠ ABC вписанный в окружность.
Углы, вписанные в окружность. Свойство
Теорема
Угол, вписанный в окружность, равен половине соответствующего центрального угла.
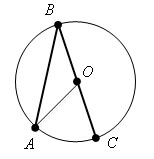
Доказательство.
Пусть есть окружность с центром в точке O и угол ABC, вписанный в эту окружность, так что одна из сторон угла проходит через центр окружности.
Соединим точку A с центром окружности точкой O. Δ ABO равнобедренный (BO=AO как радиусы). Следовательно, ∠OBA = ∠OAB. Внешний угол при вершине O, угол AOC равен сумме углов OBA и OAB. Значит
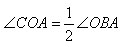
В общем случае может быть два варианта, когда стороны угла не проходят через центр окружности. Проведем вспомогательный диаметр BD
Вариант 1:
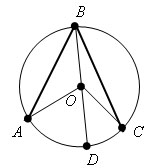
Тогда
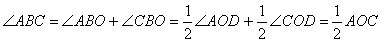
Вариант 2:
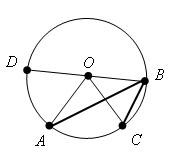
Тогда
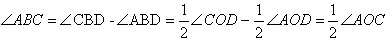
Теорема доказана.
Пропорциональность отрезков хорд
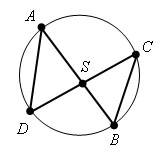
Если хорды AB и CD окружности пересекаются в точке S, то
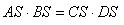 |
|
|
|
|
|
|
|
Комментариев нет:
Отправить комментарий