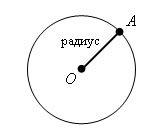
Окружностью называется геометрическая фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки плоскости. Эта точка называется центром окружности. Отрезок, соединяющий любую точку окружности с ее центром, а также его длина, называетсярадиусом окружности. AO – радиус.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром.
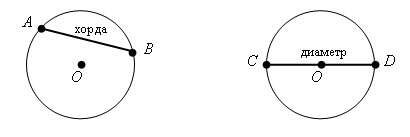
AB – хорда, CD – диаметр.
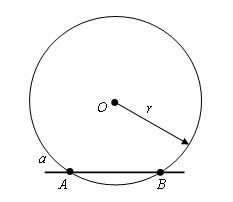
Прямая, имеющая единственную общую точку с окружностью, называется касательной, а их общая точка – точкой касания. Pадиус, проведенный в точку касания, перпендикулярен касательной.
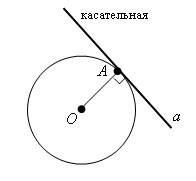
a – касательная, OA ⊥ a.
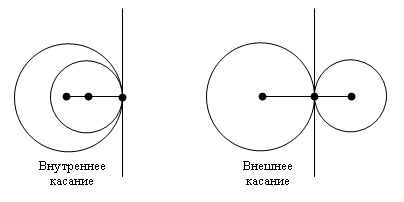
Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Через точку касания можно провести касательную к одной из окружностей, которая является одновременно и касательной к другой окружности. Касание окружностей бывает внутренним и внешним.
Касание называется внутренним, если центры окружностей лежат по одну сторону от касательной.
Касание называется внешним, если центры окружностей лежат по разные стороны от касательной
Теорема.
Диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен ей.
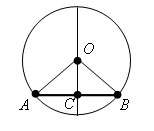
Доказательство.
Пусть AB – хорда окружности и C – ее середина. Треугольник AOB – равнобедренный с основанием AB, так как AO = OB как радиусы. По свойству медианы равнобедренного треугольника, проведенной к основанию, отрезок OC является высотой. Поэтому диаметр окружности, проведенный через середину хорды, перпендикулярен хорде. Теорема доказана.
Теорема.
Прямая, проведенная через центры касающихся окружностей, проходит через точку их касания.
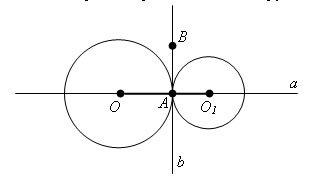
Доказательство.
Соединим центры окружностей с точкой их касания. Получим два отрезка OA и O1A. Через точку A касания двух окружностей проходит общая касательная b к этим окружностям. Пусть B точка на прямой b. Тогда ∠ BAO1 = ∠ BAO = 90 °. Следовательно, угол OAO1 – развернутый и точки O, A, O1 лежат на одной прямой a, перпендикулярной к касательной b. Теорема доказана.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
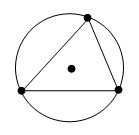
Теорема.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.

Доказательство.
Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OB как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника. Теорема доказана.
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром или медиатрисой.
Теорема.
Серединные перпендикуляры к двум сторонам треугольника пересекаются.
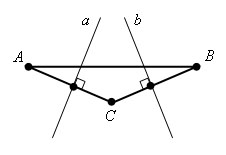
Доказательство.
Пусть есть Δ ABC и прямые a, b - серединные перпендикуляры к сторонам этого треугольника.
Допустим, прямые a и b не пересекаются, а значит a || b. AC ⊥ a, BC ⊥ b, а значит BC ⊥ a, так как a || b. Таким образом, обе прямые AC и BC ⊥ a, а значит параллельны. А это не верно, так как AC и BC пересекаются в точке С. Мы пришли к противоречию. Теорема доказана.
Окружность называется вписанной в треугольник, если она касается через все его сторон.
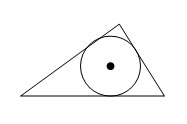
Теорема.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
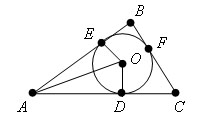
Доказательство.
Пусть ABC данный, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Δ AEO = Δ AOD по гипотенузе и катету (EO = OD – как радиус, AO – общая). Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
В задачах на построение речь идет о построении геометрических фигур (отрезок, угол, пара параллельных прямых и т. д.) с помощью чертежных инструментов. Обычно такими инструментами являются линейка, циркуль и карандаш.
Решить задачу на построение – это значит найти способ построения фигуры, осуществить это построение и доказать, что построенная фигура – фигура, обладающая требуемыми свойствами.
С помощью линейки, как инструмента геометрических построений можно:
С помощью циркуля можно:
Научившись строить «основные» геометрические фигуры, можно будет строить и более сложные, после анализа сложных и сведения их к «основным» геометрическим фигурам.
Построить треугольник с данными сторонами a, b, c.

Решение.

С помощью линейки проводим произвольную прямую и отмечаем на ней точку B.
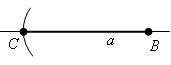
Раствором циркуля, равным a, описываем окружность с центром B и радиусом a. Пусть С точка пересечения окружности с прямой.
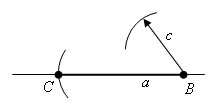
Теперь раствором циркуля, равным с, описываем окружность из центра B
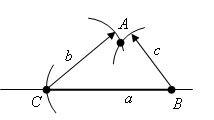
Теперь раствором циркуля, равным b, описываем окружность из центра С. Пусть A – точка пресечения этих окружностей.
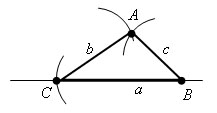
Проведем отрезки CA и BA. Поученный Δ ABC имеет стороны, равные a, b и с.
Отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.
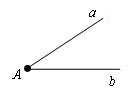
Решение.
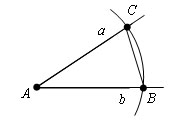
Проведем окружность с произвольным радиусом и центров в вершине A данного угла. Пусть В и С – точки пересечения окружности со сторонами угла. И проведем отрезок BC.
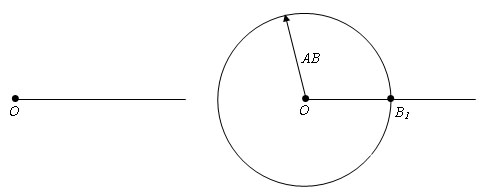
Проведем окружность радиусом AB с центром в точке О – начальной точке данной полупрямой. Точку пересечения окружности с лучом обозначим B1.
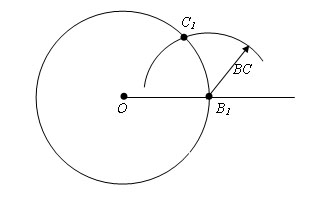
Теперь опишем окружность с центром B1 и радиусом BC. Пусть точка С1 пересечение построенных окружностей в указанной полуплоскости.
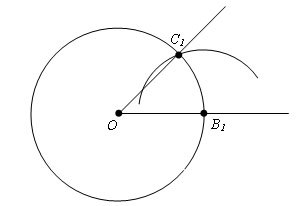
Проведем луч из точки O, через точку С1. Угол C1OB1 и будет искомый.
Доказательство.
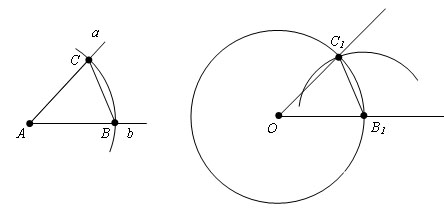
Треугольники ABC и OB1C1 равны как треугольники с соответствующими сторонами. И следовательно углы CAB и C1OB1 равны.
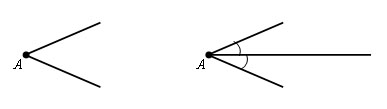
Построить биссектрису данного угла.
Решение
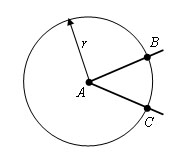
Из вершины A данного угла как из центра описываем окружность произвольного радиуса r. Пусть B и С – точки ее пересечения со сторонами угла.
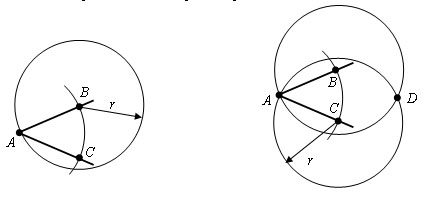
Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения отличная от A.
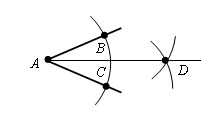
Проведем луч AD.
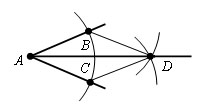
Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC.

Разделить отрезок пополам.
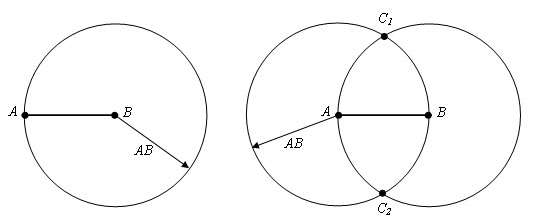
Пусть AB данный отрезок. Описываем окружность радиусом AB с центром в точках A и B. Пусть эти окружности пересекаются в точках С1 и С2.
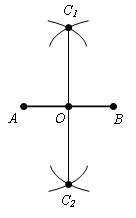
Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB.
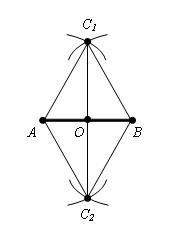
Доказательство. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 - общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB.
Через точку O провести прямую, перпендикулярную данной прямой a.
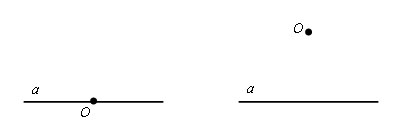
Возможно два варианта:
1. точка O лежит на прямой a;
2. точка О не лежит на прямой a.
Решение.
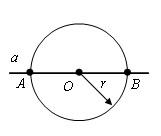
Первый вариант.
Проводим окружность с произвольным радиусом r с центром в точке O. Окружность пересекает прямую в точках A и B.
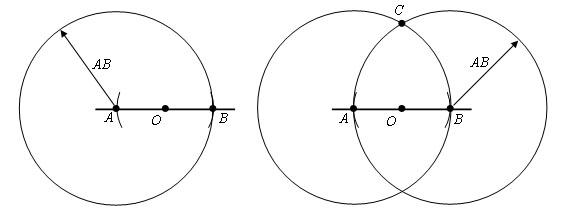
Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.
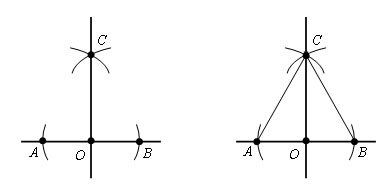
Искомая прямая проходит через точки С и О.
Доказательство.
Проведем отрезки AC и CB. Δ ACO = Δ BCO по третьему признаку равенства треугольников (AO = OB, AC = CB, по построению, CO – общая). ∠ COA = ∠ COB = 90 °. Прямая CO ⊥ AB.
Второй вариант.
Из точки O проводим окружность некоторым радиусом r, таким чтобы окружность пересекала прямую a. Пусть A и B – точки пересечения окружности с прямой a.
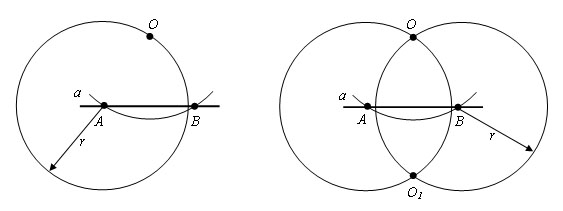
Проведем окружности тем же радиусом r с центрами в точках A и B. Пусть точка O1 – точка пресечения этих окружностей, лежащая в полуплоскости, отличной от той, в которой лежит точка O.
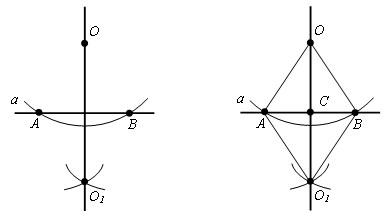
Проведем через точки O и O1 прямую. Это и будет искомая прямая. Доказательство. Пусть прямые OO1 и AB пересекаются в точке С. Δ AOB = Δ BO1A по третьему признаку равенства треугольников (AO = OB = AO1 = O1B, по построению, AB – общая). Отсюда следует, что ∠ OAС = ∠ O1AC. Δ OAC = Δ O1AC по первому признаку равенства треугольников (AO = AO1, по построению, ∠ OAС = ∠ O1AC, AС – общая). Следовательно ∠ OСA = ∠ O1CA, а так как эти углы смежные, то они прямые. Поэтому OC – перпендикуляр, опущенный из точки O на прямую a.
Даны отрезки a, b, c. Построить отрезок x = bc/a .
Решение.
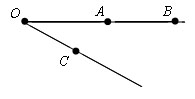
Построим любой неразвернутый угол с вершиной O. На одной стороне угла отложим отрезки OA = a, OB = b, а на другой – отрезок OC = c.
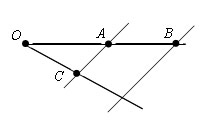
Соединим точки A и C, а через точку B проведем прямую, параллельную (AC).
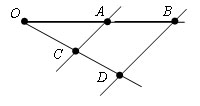
Пусть D – точка пересечения этой прямой с лучом OC. Отрезок OD – искомый.
Доказательство.
По теореме о пропорциональных отрезках: OA/OB = OC/OD
Поэтому OD = OB*OC/OA = b*c/a есть искомый отрезок x.
Построенный отрезок называется четвертым пропорциональным, потому что является четвертым членом пропорции a : b = с : x.
Комментариев нет:
Отправить комментарий