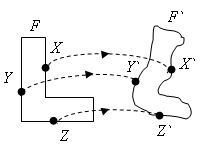
Если каждую точку данной фигуры сместить каким-нибудь образом, то получается новая фигура. Одна фигура получена из другой преобразованием.
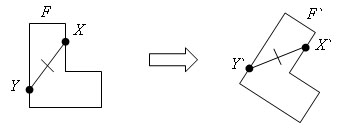
Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Такое преобразование переводит две любые точки X и Y одной фигуры в точки X` и Y` другой фигуры так, что XY = X`Y`.
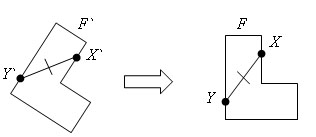
Преобразование, обратное движению, также является движением.
Теорема.
Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Доказательство.
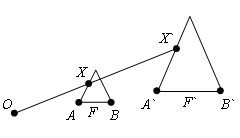
Пусть есть три точки A, B и С, которые лежат на одной прямой и точка B лежит между точками A и С.
Докажем, что точки A`, B` и C` лежат на одной прямой.
Если точки A`, B` и C` не лежат на одной прямой, то эти точки являются вершинами треугольника. Поэтому A`C`Докажем, что B` лежит между A` и C`. Тогда выполняются равенства AB=A`B`, AC=A`C`, BC=B`C`, AB+BC=AC. Отсюда следует, что A`B`+B`C`=A`C`. Это означает, что точка B` лежит между точками A` и C`.Теорема доказана.
Следствие из теоремы
1.Отрезок движением переводится в отрезок.
2.Луч при движении переходит в луч, прямая – в прямую.
3.Треугольник движением переводится в треугольник.
Теорема.
При движении сохраняются углы между полупрямыми.
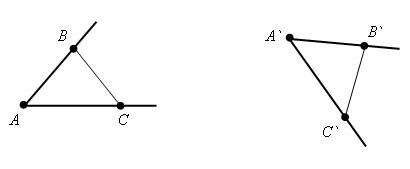
Пусть полупрямые AB и BC не лежат на одной прямой и образуют угол. При движении полупрямые переходят в A`B` и A`C` соответственно. Проведем отрезок BC и B`C`. Получим треугольник ABC и A`B`C`. Так как при движении расстояния сохраняются, то треугольники ABC и A`B`C` равны по третьему признаку равенства треугольников, а следовательно углы ABC и A`B`C` равны. Теорема доказана
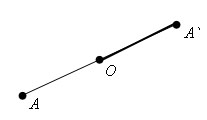
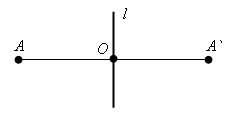
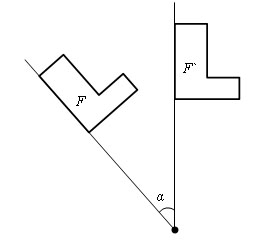
Есть O – фиксированная точка и точка A – произвольная точка. Проведем прямую через точки AO. Отложим от точки O отрезок OA` равный OA, так чтобы OA и OA` были дополнительными. Тогда точка A` называется симметричной точке A относительно точки O.
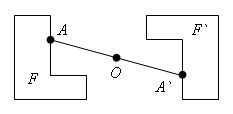
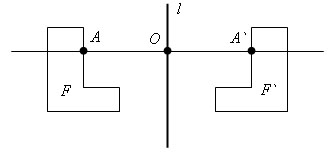
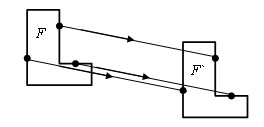
Преобразование фигуры F в фигуру F`, при котором каждая ее точка A переходит в точку A`, симметричную относительно данной точки O, называется преобразованием симметрии относительно точки O. Тогда фигуры F и F` называются симметричными относительно точки O.
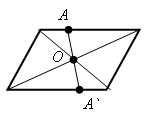
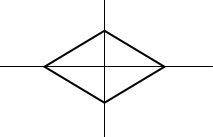
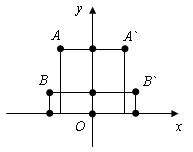
Если преобразование симметрии переводит фигуру в саму себя, то такая фигура называется центрально-симметричной. Параллелограмм – центрально-симметричная фигура.
|
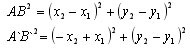
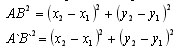
Комментариев нет:
Отправить комментарий