Объемы и поверхности тел вращения.

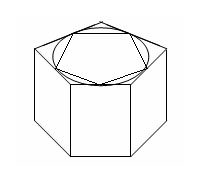
Объем цилиндра Данное тело имеет объем V, если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколь угодно мало отличающимися от V.    Найдем объем цилиндра с радиусом основания R и высотой H.  Построим две прямые призмы с высотой H такими, что основание одной призмы является n-угольник, содержащий круг, а основание второй призмы n-угольник, содержащийся в круге. Тогда первая призма содержит цилиндр, а вторая призма содержится в цилиндре. При неограниченном увеличении n площади многоугольников приближаются к площади круга S(основанию цилиндра) и, следовательно, их объемы неограниченно приближаются к SH. Тогда    Объем цилиндра равен произведению площади основания на высоту. 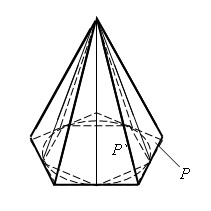Объем конуса   Построим два многоугольника в плоскости основания конуса: многоугольник P, содержащий основание конуса, и многоугольник P`, содержащийся в основании конуса. Построим две пирамиды с основаниями P и P` и вершиной в вершине конуса. Первая пирамида содержит конус, а вторая пирамида содержится в конусе.  Существуют такие многоугольники P и P`, площади которых при неограниченном увеличении числа их сторон n неограниченно приближаются к площади круга в основании конуса. Для таких многоугольников объемы построенных пирамид неограниченно приближаются к 1/3 SH, где S – площадь основания конуса, а H – его высота. 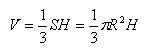Согласно определению отсюда следует, что объем конуса    Объем конуса равен одной трети произведения площади основания на высоту. 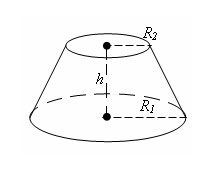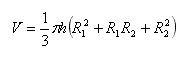Объем усеченного конуса   Пусть есть усеченный конус с радиусами оснований R1 и R2 (R2 Тогда объем усеченного конуса равен:    Общая формула для объемов тел вращения Тело вращения в простейшем случае называется такое тело, которое плоскостями, перпендикулярными оси вращения, пересекаются по кругам с центрами на этой прямой.    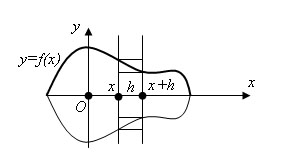Проведем плоскость через ось тела и введем в этой плоскости декартовы координаты x, y, приняв ось тела за ось x. Плоскость xy пересекает поверхность тела по линии, для которой ось x является осью симметрии. Пусть y = f(x) – уравнение той части этой линии, которая расположена над осью x.  Проведем через точку (x,0) плоскость, перпендикулярную оси x, и обозначим через V(x) объем части тела, лежащей слева от этой плоскости; V(x) является функцией от x. Разность V(x+h) – V(x) представляет собой объем слоя тела толщиной h, заключенного между двумя плоскостями, которые перпендикулярны оси x и проходят через точки с абсциссами x и x+h. Пусть M – наибольшее, а m – наименьшее значение функции f(x) на отрезке [x,x+h]. Тогда рассматриваемый слой тела содержит цилиндр с радиусом m и высотой h и содержится в цилиндре с радиусом M и той же высотой h.  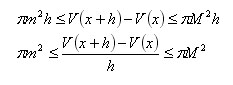Поэтому    При стремлении высоты h к нулю левая и правая части последнего неравенства стремятся к одной и той же величине πf^2(x). Средняя же часть этого неравенства при стремлении h к 0 стремится к производной V`(x) функции V(x). 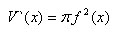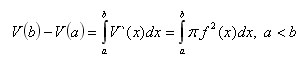Значит,    По формуле анализа    Эта формула и дает объем части тела, заключенной между параллельными плоскости x=a и x=b. Объем шара Применяя формулу для объема тел вращения вычислим объем шара.    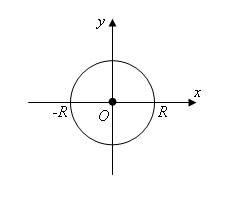Введем декартовы координаты, приняв центр шара за начало координат. 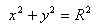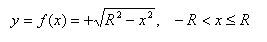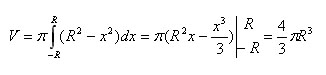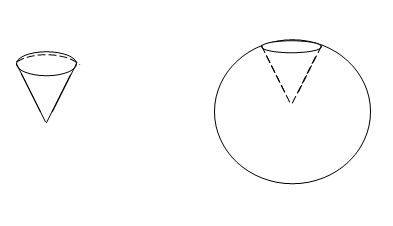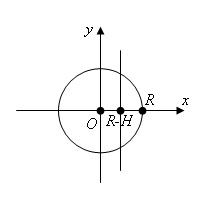Плоскость xy пересекает поверхность шара радиуса R по окружности, которая задается формулой    Полуокружность, расположенная над осью x, задается уравнением    Поэтому объем шара определяется по формуле  Объем шарового сегмента Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.  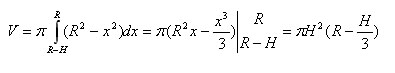Формулу для объема шарового сегмента получаем аналогично формуле объема шара:    где R – радиус шара, а H – высота шарового сегмента.  Объем шарового сектора Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется. Объем шарового сектора получается сложением или вычитанием объемов соответствующих сегмента и конуса. 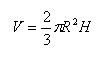Для объема шарового сектора получается следующая формула:    где R – радиус шара, а H – высота соответствующего шарового сегмента..  Площадь боковой поверхности цилиндра <Впишем в цилиндр правильную n-угольную призму. Площадь боковой поверхности этой призмы Sn=PnH, где Pn – периметр основания призмы, а H – ее высота.  При неограниченном увеличении n периметр Pn неограниченно приближается к длине С окружности основания цилиндра. Следовательно, площадь боковой поверхности призмы неограниченно приближается к CH. Поэтому величина CH принимается за площадь боковой поверхности цилиндра.  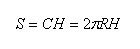Площадь боковой поверхности цилиндра вычисляется по формуле    где R – радиус цилиндра, а H – его высота.  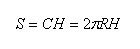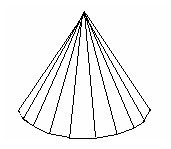Площадь боковой поверхности конуса   Впишем в конус правильную n-угольную пирамиду. Площадь боковой поверхности.    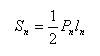где Pn – периметр основания пирамиды, а ln – апофема.  При неограниченном увеличении n периметр основания Pn неограниченно приближается к длине С окружности основания конуса, а апофема ln – к длине l образующей. Соответственно боковая поверхность пирамиды неограниченно приближается к 0.5Cl. В связи с этим величина 0,5Cl принимается за площадь боковой поверхности конуса.  Площадь боковой поверхности конуса вычисляется по формуле    где R – радиус основания конуса, а l – длина образующей.  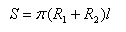Для площади боковой поверхности усеченного конуса с радиусами оснований R1, R2 и образующей l получается формула  Площадь сферы   Опишем около сферы выпуклый многогранник с малыми гранями. Пусть S` - площадь поверхности многогранника, т.е. сумма площадей его граней. Найдем приближенное значение площади поверхности многогранника, предполагая, что линейные размеры граней, т.е. расстояние между любыми двумя точками любой грани, меньше ε.  Объем многогранника равен сумме объемов пирамид, имеющих своими основаниями грани многогранника, а вершиной – центр сферы. 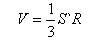Так как все пирамиды имеют одну и ту же высоту, равную радиусу R сферы, то объем многогранника    Объем многогранника больше объема шара, ограниченного сферой, но меньше объема шара с тем же центром и с радиусом R+ε. 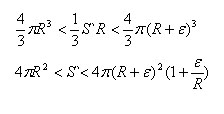Таким образом,    Площадь поверхности описанного многогранника при неограниченном уменьшении размеров его граней, т.е. при неограниченном уменьшении ε, стремится к 4πR^2 и поэтому эта величина принимается за площадь сферы.  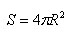Площадь сферы радиуса R вычисляется по формуле    Аналогично определяется площадь сферической части поверхности шарового сектора, т.е. 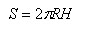площадь сферического сегмента, для нее получается формула    где H – высота сегмента.