Теорема Пифагора.

Косинус угла

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 

 

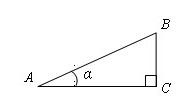
Косинус угла α обозначается: cos α. 

 

Теорема 

Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника. 

 

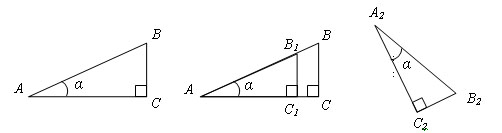
Доказательство. 

Пусть даны Δ ABC и Δ A2B2C2 – прямоугольные треугольники. ∠ A = ∠ A2 = ∠ α. Требуется доказать, что 

 

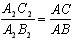
Построим Δ AB1C1, равный A2B2C2. Прямые B1C1 и BC перпендикулярны AC и следовательно параллельны между собой. Тогда, по теореме о пропорциональных отрезках 

 

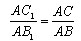
А поп построению A2C2 = AC1 и A2B2 = AB1, то 

 

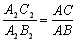
Теорема доказана.


Теорема Пифагора

Теорема. 

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 

 

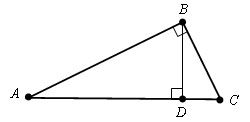
Доказательство. 

Пусть Δ ABC прямоугольный и ∠ ABC – прямой. 
Проведем высоту BD из вершины B прямого угла. По определению косинуса угла 

 

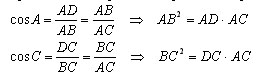
Сложим получены равенства почленно: 

 

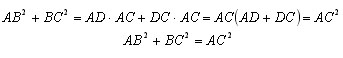
Теорема доказана.

Неравенство треугольника

Теорема. 

Каковы бы не были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. 

Доказательство. 

Пусть A, B и С – данные три точки. 

 

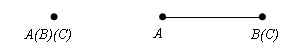
Если две токи из трех или все три точки совпадают, то утверждение теоремы очевидно. 

 

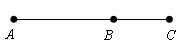
Если все точки различны и лежат на одной прямой, то AB + BC = AC. Отсюда видно, что каждое из трех расстояний не больше суммы двух других. 

 

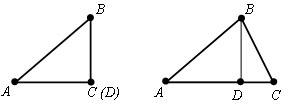
Если три точки не лежат на одной прямой докажем, что AC

Синус и тангенс угла

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. 

 

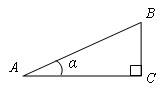
Синус угла α обозначается: sin α. 

 

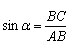
Тангенсом угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Тангенс угла α обозначается: tg α. 

 

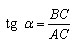
Теорема. 

Cинус и танегнс угла так же, как и косинус, зависят только от величины угла. 

Доказательство.

Пусть ABC данный прямоугольный треугольник, тогда по теореме Пифагора 

 

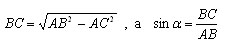
, a 

 

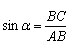
Тогда 

 

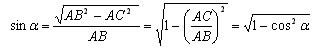
А так как cos зависит только от величины, то sin тоже зависит только от величины. 

 

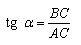
Разделим числитель и знаменатель на AB: 

 

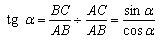
А так как cos и sin зависят только от величины угла, то tg тоже зависит только от величины угла. Теорема доказана.