Теорема.
Сумма углов треугольника равна 180º.
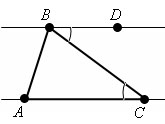
Доказательство. Пусть дан треугольник ABC. Проведем через вершину B прямую, параллельную прямой AC. Отметим на полученной прямой точку D так, чтобы она лежала в другой полуплоскости относительно прямой BC.
∠ CAB и ∠ ABD – внутренние односторонние углы для параллельных прямых AC и BD с секущей AB, тогда:
∠ CAB + ∠ ABD = 180º ⇒ ∠ ABD = 180º - ∠ CAB
∠ ABD = ∠ ABC + ∠ CBD.
Так как ∠ CBD = ∠ ACB как внутренние накрест лежащие, образованные пересечением параллельных прямых BD и AC c секущей BC, то
∠ ABD = ∠ ABC + ∠ ACB
Приравниваем ∠ ABD:
∠ ABC + ∠ ACB = 180º - ∠ CAB
И ∠ ABC + ∠ ACB + ∠ CAB = 180º
Теорема доказана.
Из теоремы следует:
У любого треугольника хотя бы два угла острые.
Доказательство.
Допустим, что у треугольника один угол острый или вообще нету. Тогда, по крайней, у этого треугольника два тупых угла. А градусная мера тупого угла больше 90º. Значит сумма двух тупых углов уже будет больше 180º. А это невозможно, так как сумма всех углов треугольника 180º. Что и требовалось доказать.
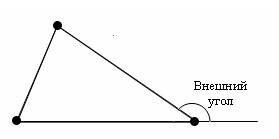
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
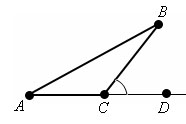
Доказательство. Пусть ABC – данный треугольник. По теореме о сумме углов в треугольнике
∠ ABС + ∠ BCA + ∠ CAB = 180 º.
Отсюда следует
∠ ABС + ∠ CAB = 180 º - ∠ BCA = ∠ BCD
Теорема доказана.
Из теоремы следует:
Внешний угол треугольника больше любого угла треугольника, не смежного с ним.
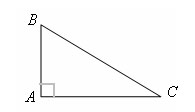
Треугольник называется прямоугольным, если у него есть прямой угол. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны – катетами. AC и AB – катеты, BC – гипотенуза.
Теорема.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
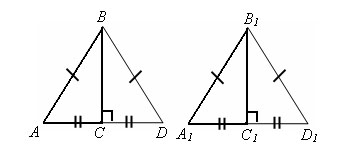
Доказательство.
Пусть ABC и A1B1C1 – данные треугольники. Построим треугольник DBC равный треугольнику ABC, и треугольник D1B1C1 равный треугольнику A1B1C1.
Δ ABD = Δ A1B1D1 по третьему признаку равенства треугольников (AB=A1B1, BD=B1D1, AD=A1D1) из этого следует, что ∠ BAC = ∠ B1A1C1.
Δ ABC = Δ A1B1C1 по первому признаку равенства треугольников (AB=A1B1, AC=A1C1, Δ ABC = Δ A1B1C1). Теорема доказана.
Теорема.
Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Доказательство
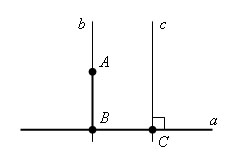
Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.
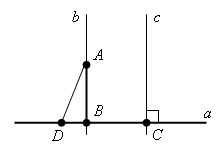
Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.
Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от дочки до прямой.
Теорема.
Расстояние от любых двух точек прямой до параллельной прямой равны.
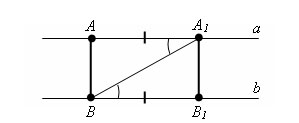
Пусть а и b – параллельные прямые и точки A и A1 – некоторые точки на прямой a. Опустим из точки A перпендикуляр AB на прямую b и отложим из точки B отрезок BB1, равный AA1 так, что бы A и B1 были по разные стороны от прямой A1B.
Δ A1AB = Δ BB1A1 по первому признаку равенства треугольников (A1B – общая, ∠ AA1B = ∠ B1BA1 – как внутренние накрест лежащие, AA1=B1B).
Из равенства треугольников следует, что A1B1 тоже перпендикуляр к прямой b и AB = A1B1. Теорема доказана.
Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Комментариев нет:
Отправить комментарий