Тела вращения.

Цилиндр   Доказательство  Цилиндром называется тело, которой стоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра.  Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.  Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Цилиндр. Свойства 1. Основания цилиндра равны, так как при параллельный перенос есть движение.  2. У цилиндра основания лежат в параллельных плоскостях, так как при параллельном переносе плоскость переходит в параллельную плоскость.  3. У цилиндра образующие параллельны и равны, так как при параллельном переносе точки смещаются по параллельным прямым на одно и тоже расстояние. 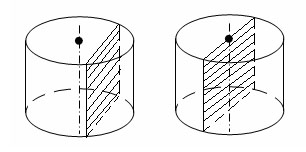Сечение цилиндра плоскостью   Сечение цилиндра плоскостью, параллельной его оси, представляет прямоугольник.  Осевым сечением называется сечение, которое проходит через ось цилиндра.  Теорема  Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.    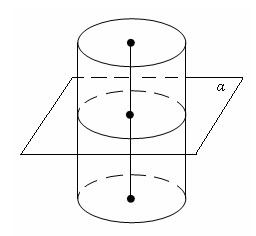Доказательство  Пусть α – плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещает плоскость α с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью α с окружностью основания. Теорема доказана. 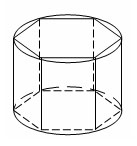Вписанная и описанная призмы   Призмой, вписанной в цилиндр, называется такая призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.    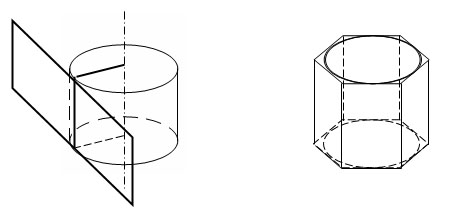Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.  Призмой, описанной около цилиндра, называется призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра. 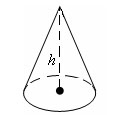Конус   Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.  Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.  Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Сечение конуса плоскостями Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса    Теорема  Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.    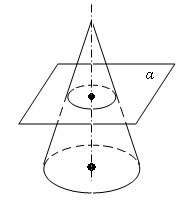Доказательство  Пусть α – плоскость, параллельная плоскости основания конуса и пересекающая конус. Преобразование гомотетии относительно вершины конуса, совмещающее плоскость α с плоскостью основания, совмещает сечение конуса плоскостью α с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана.  Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший кусок. Оставшаяся часть называется усеченным конусом. 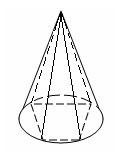Вписанная и описанная пирамиды   Пирамидой, вписанной в конус, называется такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус, являются образующими конуса.    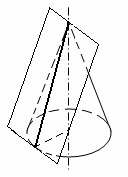Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую.    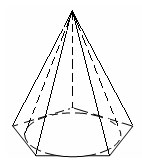Пирамида, описанной около конуса, называется пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса. 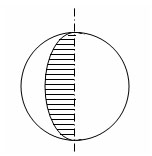Шар   Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.  Граница шара называется шаровой поверхностью, или сферой. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Сечение шара плоскостью Теорема  Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.  Доказательство  Пусть α - секущая плоскость и O – центр шара. Опустим перпендикуляр из центра шара на плоскость α и обозначим через O` основание этого перпендикуляра.  Пусть X – произвольная точка шара, принадлежащая плоскости α. 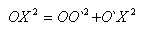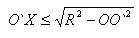По теореме Пифагора    Так как OX не больше радиуса R шара, то    т.е. 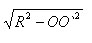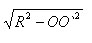любая точка сечения шара плоскостью α находится от точки O` на расстоянии, не большем    следовательно, она принадлежит кругу с центром O` и радиусом    Обратно: любая точка X этого круга принадлежит шару. А это значит, что сечение шара плоскостью α есть круг с центром в точке O`. Теорема доказана. Симметрия шара Теорема  Любая диаметральная плоскость шара является его плоскостью. Центр шара является его центром симметрии.    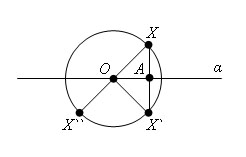Доказательство  Пусть α - диаметральная плоскость и X - произвольная точка шара. Построим точку X`, симметричную точке X относительно отрезку XX` и пересекается с ним в его середине. Из равенства прямоугольных треугольников OAX и OAX` следует, что OX` = OX.  Так как OX ≤ R, то и OX` ≤ R, т.е. точка, симметричная точке X, принадлежит шару. Первое утверждение теоремы доказано.  Пусть теперь X`` - точка, симметричная точке X относительно центра шара. Тогда OX`` = OX ≤ R, т.е. точка X`` принадлежит шару. Теорема доказана полностью. 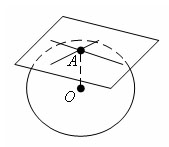Касательная плоскость к шару   Плоскость, проходящая через точку A шаровой поверхности и перпендикулярная радиусу, проведенному в точку A, называется касательной плоскостью. Точка A называется точкой касания.  Теорема  Касательная плоскость имеет с шаром только одну общую точку – точку касания.    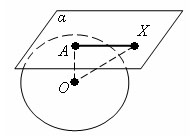Доказательство  Пусть α - плоскость, касательная к шару, и A – точка касания. Возьмем произвольную точку X плоскости α, отличную от A. Так как OA – перпендикуляр, а OX – наклонная, то OX > OA = R.  Следовательно, точка X не принадлежит шару. Теорема доказана. Пересечение двух сфер Теорема  Линия пересечения двух сфер есть окружность.    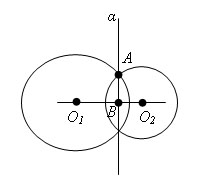Доказательство  Пусть O1 и O2 – центры сфер и A – их точка пересечения. Проведем через точку A плоскость α, перпендикулярную прямой O1O2.  Обозначим через B точку пересечения плоскости α с прямой O1O2. По теореме сечение шара плоскостью плоскость α пересекает обе сферы по окружности K с центром B, проходящей через точку A. Таким образом, окружность K принадлежит пересечению сфер.  Докажем, что сферы не имеют других точек пересечения, кроме точек окружности K. Допустим, точка X пересечения сфер не лежит на окружности K. Проведем плоскость через точку X и прямую O1O2. Она пересечет сферы по окружностям с центрами O1 и O2. Эти окружности пересекаются в двух точках, принадлежащих окружности K, да еще в точке X. Но две окружности не могут иметь больше двух точек пересечения. Следовательно, пересечение сфер есть окружность. Теорема доказана Вписанные и описанные многогранники Многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара.  Многогранник называется описанным около шара, если все его грани касаются поверхности шара.