Центральная симметрия параллелепипеда
Теорема
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
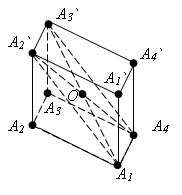
Доказательство
Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам.
Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Теорема доказана.
Объем прямоугольного параллелепипеда
Для того чтобы найти объем прямоугольного параллелепипеда с линейными размерами a, b, c докажем, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как их высоты.
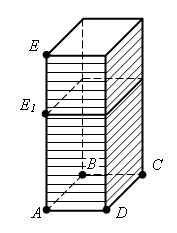
Пусть P и P1 – два прямоугольных параллелепипеда с общим основанием ABCD и высотами AE и AE1. Будем считать для определенности, что AE1 < AE. Пусть V и V1 – объемы параллелепипедов. Разобьем ребро AE параллелепипеда P на большое число n равных частей. Каждая из них равна AE/n. Пусть m – число точек деления, которые лежат на ребре AE1. Тогда
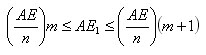
Отсюда
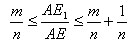
Проведем через точки деления плоскости, параллельные основанию. Они разобьют параллелепипед P на n равных параллелепипедов. Каждый из них имеет объем V/n. Параллелепипед P1 содержит первые m параллелепипедов, считая снизу, и содержится в m+1 параллелепипедах. Поэтому
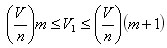
Отсюда
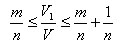
Так как V1/V и AE1/AE заключены между m/n и m/n + 1/n, то они отличаются не более чем на 1/n. А так как n можно взять сколь угодно большим, то это может быть только при
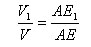
что и требовалось доказать.
Возьмем теперь куб, являющийся единицей измерения объема, и три прямоугольных параллелепипеда с измерениями: a, 1, 1; a, b, 1; a, b, c. Обозначим, их объемы V1, V2 и V соответственно. По доказанному
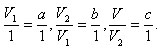
Перемножая эти равенства почленно, получим: V=abc.
Объем наклонного параллелепипеда
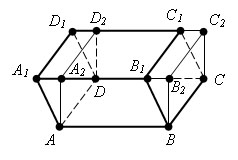
Пусть есть параллелепипед ABCDA1B1C1D1. Проведем через ребро BC плоскость, перпендикулярную основанию ABCD, и дополним наклонный параллелепипед треугольной призмой BB1B2CC1C2. Отсечем теперь от полученного тела треугольную призму плоскостью, проходящей через ребро AD и перпендикулярной основанию ABCD. Тогда получим снова параллелепипед. Этот параллелепипед имеет объем, равный объему исходного параллелепипеда.
Достроенная призма и отсекаемая совмещаются параллельным переносом на отрезок AB, следовательно, имеют одинаковые объемы. При описанном преобразовании параллелепипеда сохраняются площадь его основания и высота. Сохраняются также плоскости двух боковых граней, а две другие становятся перпендикулярными основанию.
Применяя еще раз такое преобразование к наклонным граням, получим параллелепипед, у которого все боковые грани перпендикулярны основанию, т.е. прямой параллелепипед.
Объем произвольной призмы
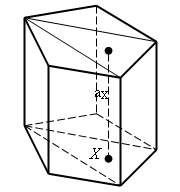
Возьмем произвольную призму. Разобьем ее основание на треугольники. Пусть Δ - один из этих треугольников. Проведем через произвольную точку X – треугольника Δ прямую, параллельную боковым ребрам. Пусть ax – отрезок этой прямой, принадлежащий призме. Когда точка X описывает треугольник Δ, отрезки ax заполняют треугольную призму. Построив такую призму для каждого треугольника Δ, получим разбиение данной призмы на треугольники. Все эти призмы имеют одну и ту же высоту, равную высоте исходной призмы.
Объем данной призмы равен сумме объемов треугольных призм, ее составляющих. По доказанному объем треугольной призмы равен произведению площади ее основания на высоту. Следовательно, объем призмы равен:
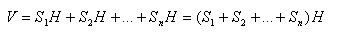
где S1, S2, …, Sn – площади треугольников, на которые разбито основание призмы, а Н – высота призмы. Следовательно, V=SH.
Объем любой призмы равен произведению площади ее основания на высоту.
Объем треугольной призмы
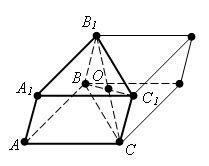
Возьмем треугольную призму и дополним ее до параллелепипеда. Точка O является центром симметрии параллелепипеда. Поэтому достроенная призма симметрична исходной относительно точки O, следовательно, имеет объем, равный объему исходной призмы. Таким образом, объем построенного параллелепипеда равен удвоенному объему данной призмы.
Объем параллелепипеда равен произведению площади его основания на высоту. Площадь его основания равна удвоенной площади треугольника ABC, а высота равна высоте исходной призмы. Отсюда заключаем, что объем исходной призмы равен произведению площади ее основания на высоту.
Объем треугольной пирамиды
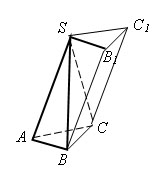
Пусть SABC – треугольная пирамида с вершиной S и основанием ABC. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма составлена из трех пирамид: данной пирамиды SABC и еще двух треугольных пирамид SCC1B1 и SCBB1.
У второй и третьей пирамид равные основания - ΔCC1B1 и ΔB1BC и общая высота, проведенная из вершины S. Поэтому у них равные объемы.
У первой и третьей пирамид тоже равные основания - ΔSAB и ΔBB1S и совпадающие высоты, проведенные из вершины C. Поэтому у них тоже равные объемы.
Значит, все три пирамиды имеют один и тот же объем. Так как сумма объемов равна объему призмы, то объемы пирамид равны SH/3.
Объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:
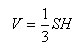
Объем произвольной пирамиды
Есть произвольная пирамида. Разобьем ее основание на треугольники Δ1, Δ 2, …, Δn. Пирамиды, у которых основаниями являются эти треугольники, а вершинами – вершина данной пирамиды, составляют данную пирамиду. Объем данной пирамиды равен сумме объемов составляющих ее пирамид. Так как все они имеют ту же высоту H, что и данная пирамида, то объем ее равен:
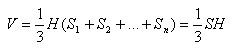
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту.
Объем усеченной пирамиды
Есть усеченная пирамида с площадями оснований S1 и S2 (S1>S2) и высотой h.
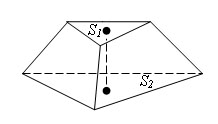
Тогда объем усеченной пирамиды равен:
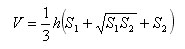 |
|
|
|
|
|


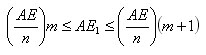
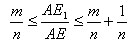
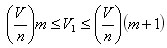
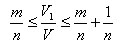
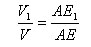
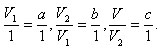


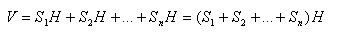


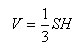
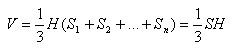

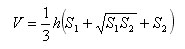
Комментариев нет:
Отправить комментарий