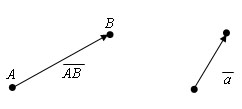
Коллинеарный вектор

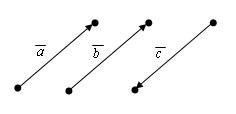
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.
Коллинеарный вектор. Свойства
Теорема
Если есть два отличных от нуля коллинеарных вектора, то существует число λ такое, что
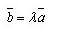
Доказательство.
Пусть a и b одинаково направлены.
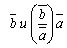
- это векторы, которые одинаково направлены и имеют одну и ту же абсолютную величину |b|. Значит, они равны:
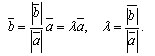
Когда векторы a и b противоположно направлены аналогично заключаем, что
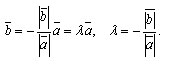
Теорема доказана.
Теорема
Любой вектор с можно представить в виде
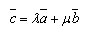
Координаты вектора
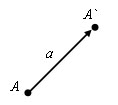
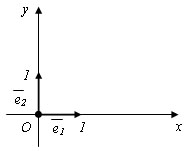
Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2).
Абсолютная величина вектора a (a1; a2) равна
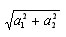
Если начало вектора совпадает с его концом, то это нулевой вектор , обозначается (0).
Координаты вектора. Свойства
Теорема
Равные векторы имеют равные соответствующие координаты.
Доказательство
Рассмотрим два случая: 1) векторы не лежат на одной прямой.
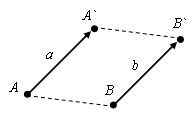
Пусть есть вектор a с началом в точке A (x; y) и концом в точке A` (x`; y`). При параллельном переносе получаем вектор b, у которого тогда начало будет в точке B(x+c; y+d), а конец в точке B`(x`+c; y`+d). Отсюда видно, что оба вектора будут иметь одни и тебе координаты (x-x`; y-y`).
2) векторы лежат на одной прямой.
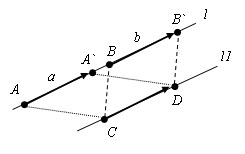
Пусть есть прямая l на которой лежат равные векторы AA` и BB`. A(x; y), A`(x`; y`), B(x1;y1) и B(x1`; y1`). Проведем прямую l1 параллельную l и отложим на ней вектор CD равный AA` и BB`, C (x0; y0) и D (x0`; y0`). Так как AA` = CD, из предыдущего пункта x-x`=x0-x0` и y-y`=y0-y0`. С другой стороны BB` = CD и x1-x1`=x0-x0`, y1-y1`=y0-y0`. Сравнивая равенства получаем x-x`=x1-x1` и y-y`=y1-y1`. Теорема доказана.
Равенство векторов
Два вектора называются равными, если они совмещаются параллельным переносом.
Т.е. существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно.
Теорема
Если векторы одинаково направлены и равны по абсолютной величине, то они равны.
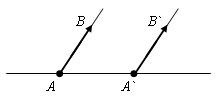
Доказательство.
Пусть AB и CD – одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку A` в точку A, совмещает луч A`B` с лучом AB, потому что они сонаправлены. Отрезка AB и A`B` равны, поэтому точка B совмещается с точкой B`. Значит, параллельный перенос переводит вектор A`B` в вектор AB. Значит векторы равны. Теорема доказана.
Скалярное произведение
Скалярным произведением векторов a (a1; a2) и a (b1; b2) называется число a1b1+a2b2.
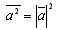
Для любых векторов a (a1; a2), b (b1; b2), c (с1; с2)
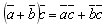
Углом между ненулевыми векторами AB и AC называется угол ABC. Углом между любыми двумя ненулевыми векторами a и b называется угол между равными им векторами с общим началом.
Скалярное произведение. Свойство
Теорема
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
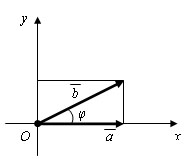
Доказательство.
Пусть a и b – данные векторы и φ – угол между ними. Имеем:
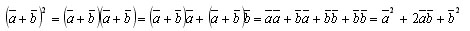
или
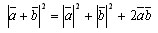
Скалярное произведение ab таким образом, выражается через длины векторов a, b и a + b т. е. систему координат можно выбрать любую, а величина скалярного произведения не изменится. Выберем систему координат xy так, чтобы начало координат совпало с началом вектора a, а сам вектор лежал на положительной полуоси оси Ox. Тогда координатами вектора a будут числа |a| и 0, а координатами вектора a – |a| cos φ и |a| sin φ . По определению
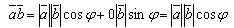
Теорема доказана.
Из теоремы следует, что
если векторы перпендикулярны, то их скалярное произведение равно нулю.
Сложение векторов
Суммой векторов a(a1; a2) и b(b1; b2) называется вектор c(a1+b1; a2+b2).
Для любых векторов a(a1; a2), b(b1; b2), c(с1; с2) справедливы равенства:
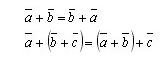
Теорема
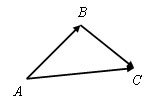
Каковы бы ни были три точки A, B и C, имеет место векторное равенство
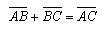
Доказательство.
Пусть A(x1; y1), B(x2; y2), C(x3; y3) – данные три точки.
Вектор AB имеет координаты (x2 – x1; y2 – y1), вектор BC имеет координаты (x3 – x2; y3 – y2). Следовательно, вектор AB + BCимеет координаты (x3 – x1;y3 – y1). А вектор AC имеет координаты (x3 – x1;y3 – y1). Значит, AC = AB+ BC. Теорема доказана.
Сложение векторов. Правило параллелограмма
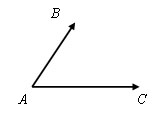
Правилом параллелограмма сложения векторов называется следующий способ:
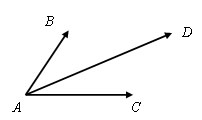
Пусть есть векторы AB и AC у которых начало вектора совпадает, а концы не совпадают
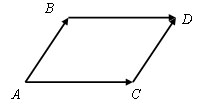
Достроим данный угол до параллелограмма, так что AC = BD и AB = CD.
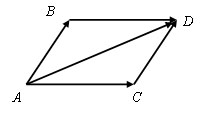
Тогда AB + BD = AD, а так как BD = AC, то AB + AC = AD
Сложение векторов. Правило треугольника
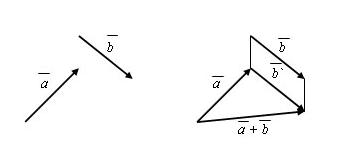
Правилом треугольника сложения векторов называется следующий способ:
Пусть есть произвольные векторы a и b. Надо от конца вектора a отложить вектор b`, равный вектору b. Тогда вектор, начало которого совпадает с началом вектора a, а конец совпадет с концом вектора b`, будет суммой a + b.
Сложение векторов. Разность
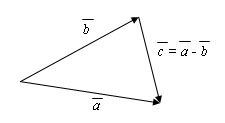
Разностью векторов a(a1; a2) и b(b1; b2) называется такой вектор c, который в сумме с вектором b дает вектор a:
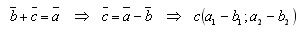
Свойство умножения вектора на число
Теорема
Абсолютная величина вектора λa равна |λ| |a|. Направление вектора λa при a≠ 0 совпадает с направлением вектора a, если λ>0, и противоположно направлению вектора a, если λ<0.
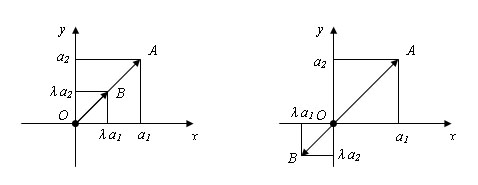
Доказательство.
Построим векторы OA и OB равные a и λa соответственно (O – начало координат). Пусть a1 и a2 – координаты вектора a. Тогда координатами точки A будут числа a1 и a2 координатами точки B – числа λa1 и λa2. Уравнение прямой OA имеет вид: αx + βy = 0.
Так как уравнению удовлетворяют координаты точки A (a1; a2), то ему удовлетворяют и координаты точки B (λa1; λa2). Отсюда следует, что точка B лежит на прямой OA. Координаты c1 и c2 любой точки C, лежащей на луче OA, имеют те же знаки, что и координаты a1 и a2 точки A, и координаты любой точки, которая лежит на луче, дополнительном к OA, имеют противоположные знаки.
Поэтому, если λ > 0, то точка B лежит на луче OA, а следовательно, векторы a и λa одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы a и λa противоположно направлены.
Абсолютная величина вектора λa равна:
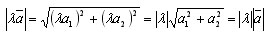
Теорема доказана.
Умножение вектора на число
Произведение вектора a(a1; a2) на число λ называется вектор (λa1; λa2), т.е. (a1; a2) λ = (λa1; λa2).
Для любого вектора a и чисел λ, μ
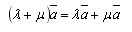
Для любого вектора a и b и числа λ
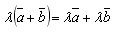 |
|
|
|
|
|
|
|
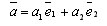

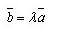
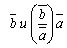
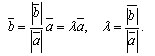
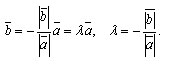
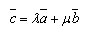

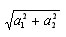



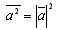
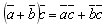

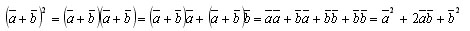
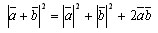
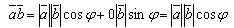
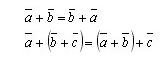

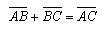






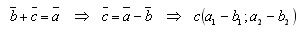

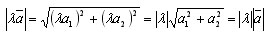
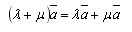
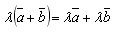
Комментариев нет:
Отправить комментарий