Четырех угольником называется фигура, которая состоит из четырех точек (вершины четырехугольника) и четырех последовательно соединяющих эти точки отрезков (стороны четырехугольника). При этом:
1. ни какие три данные точки не лежат на одной прямой;
2. соединяющие эти точки отрезки не должны не пересекаться.
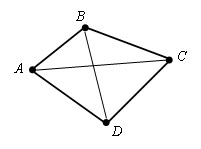
Точки A, B, C, D – вершины четырех угольника.
Отрезки AB, BC, CD, DA – стороны четырехугольника.
Вершины четырех угольника называются соседними вершинами, если они являются концами одной из его сторон. Например, вершины A и B – соседние.
Вершины, не являющиеся соседними, называются противолежащими вершинами. Например, вершины A и С – противолежащие. Отрезки, которые соединяют противолежащие вершины четырехугольника, называются диагоналями. AC и BD – диагонали четырехугольника.
Стороны четырехугольника, исходящие из одной вершины, называются соседними (смежными) сторонами. Например, AB и BC – соседние стороны. Стороны не имеющие общих вершин, называются противолежащими сторонами. Например, AB и CD – противолежащие стороны.
Четырехугольник обозначается указанием его вершин, например ABCD. В обозначение четырехугольника стоящие рядом вершины должны быть соседними. Т.е. обозначить четырехугольник ABDС нельзя (B и D – не соседние вершины).
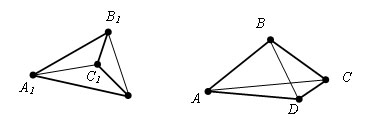
Четырехугольники A1B1C1D1 и ABCD отличаются тем, что у одного диагонали пересекаются, а у другого нет. Четырехугольники у которых диагонали пересекаются будем называть выпуклыми. Сумму длин всех сторон четырехугольника будем называть периметром. P = AB + BC + CD + DA.
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
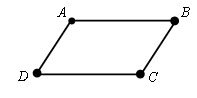
Теорема.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
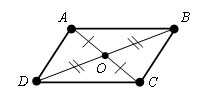
Доказательство.
Пусть ABCD – данный параллелограмм, O – точка пересечения диагоналей данного параллелограмма.
Δ AOD = Δ COB по первому признаку равенства треугольников (OD = OB, AO = OC по условию теоремы, ∠ AOD = ∠ COB, как вертикальные углы). Следовательно, ∠ OBC = ∠ ODA. А они являются внутренними накрест лежащими для прямых AD и BC и секущей BD. По признаку параллельности прямых прямые AD и BC параллельны. Так же доказываем, что AB и DC тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.
Теорема.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
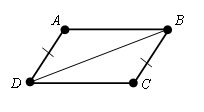
Пусть ABCD – данный четырехугольник. AD параллельно BC и AD = BC.
Тогда Δ ADB = Δ CBD по первому признаку равенства треугольников (∠ ADB = ∠ CBD, как внутренние накрест лежащие между прямыми AD и BC и секущей DB, AD=BC по условию, DB – общая).
Следовательно, ∠ ABD = ∠ CDB, а эти углы являются внутренними накрест лежащими для прямых AB и CD и секущей DB. По теореме признаке параллельности прямых AB и CD параллельны. Значит, ABCD – параллелограмм. Теорема доказана.
Теорема.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
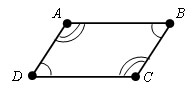
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
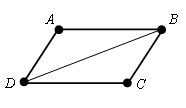
Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.
Теорема. (Свойство диагоналей параллелограмма)
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство.
Пусть ABCD – данный параллелограмм. Проведем диагональ AC. Отметим на ней середину O. На продолжении отрезка DO отложим отрезок OB1, равный DO.
По предыдущей теореме AB1CD – параллелограмм. Поэтому, прямая AB1 параллельна DC. Но через точку A можно провести только одну прямую, параллельную DC. Значит, прямая AB1 совпадает с прямой AB.
Также доказывается, что BC1 совпадает с BC. Значит, точка С совпадает с С1. параллелограмм ABCD совпадает с параллелограммом AB1CD. Следовательно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Теорема доказана.
Теорема. (Свойство противолежащих сторон параллелограмма).
У параллелограмма противолежащие стороны равны.

Доказательство.
Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.
Так как Δ AOB = Δ COD по первому признаку равенства треугольников (∠ AOB = ∠ COD, как вертикальные, AO=OC, DO=OB, по свойству диагоналей параллелограмма), то AB=CD. Точно также из равенства треугольников ВОС и DOA, следует что BC=DA. Теорема доказана.
Теорема. (Свойство противолежащих углов параллелограмма).
У параллелограмма противолежащие углы равны.

Доказательство.
Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.
Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая). Из равенства треугольников следует, что ∠ ABC = ∠ CDA.
Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана.
Прямоугольником называется параллелограмм, у которого все углы прямые.
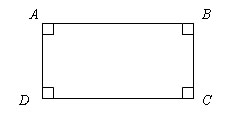
Теорема.
Если у параллелограмма все углы равны, то он является прямоугольником.
Доказательство.
Пусть дан параллелограмм ABCD и ∠ A = ∠ B = ∠ С = ∠ D.
Углы A и B являются внутренними односторонними, а значит их сумма равна 180 º. По условию они равны, значит каждый из них равен 90 º. Значит, ∠ A = ∠ B = ∠ С = ∠ D = 90 º. А параллелограмм, у которого все углы прямые, есть прямоугольник. Теорема доказана.
Теорема (свойство прямоугольника).
Диагонали прямоугольника равны.
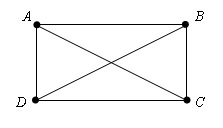
Доказательство.
Пусть ABCD – данный прямоугольник.
Δ DAB = Δ CAB по первому признаку (∠ DAB = ∠ CBA, AD=BC, как противолежащие стороны параллелограмма, AB – общая), поэтому DB=AC. Теорема доказана.
Ромб – это параллелограмм, у которого все стороны равны.
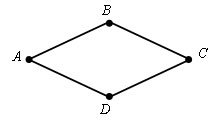
Теорема.
Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
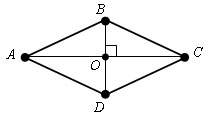
Доказательство.
Пусть ABCD – данный параллелограмм и AC ⊥ BD.
Δ AOB = Δ COB по первому признаку равенства треугольников (∠ AOB = ∠ BOC, по условию, AO = OC – по свойству диагоналей параллелограмма, BO – общая). Следовательно, AB = BC. По свойству противолежащих сторон параллелограмма AB = DC, BC = AD, т.е. все стороны равны, значит ABCD – ромб. Теорема доказана.
Теорема.
Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
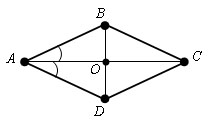
Пусть ABCD – данный параллелограмм и ∠ CAB = ∠ CAD.
∠ CAD = ∠ ACB как внутренние накрест лежащие при прямых BC и AD и секущей AC. А по условию ∠ CAB = ∠ CAD, следует что Δ ABC – равнобедренный (∠ CAB = ∠ ACB, признак равнобедренного треугольника). Поэтому, AB = BC. Так как ABCD – параллелограмм, то AB = CD, BC = AD. Тогда AB = BC = CD = AD. Таким образом, ABCD – ромб. Теорема доказана.
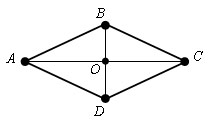
Теорема (свойства ромба).
Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.
Доказательство.
Пусть ABCD – данный ромб. Диагонали ромба пересекаются в точке O.
По свойству параллелограмма AO = OC, значит BO – медиана Δ ABC. А так как треугольник ABC - равнобедренный, то по свойствам медианы равнобедренного треугольника проведенной к основанию, BO является также высотой и биссектрисой. Значит прямая BO ⊥ AC и ∠ ABO = ∠ CBO. Теорема доказана.
Квадрат – это прямоугольник, у которого все стороны равны.
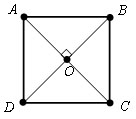
Квадрат обладает следующими свойствами:
1. у квадрата все углы прямые;
2. диагонали квадрата равны;
3. диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.
AB=BC=CD=DA
∠ A = ∠ B = ∠ C = ∠ D = 90 °
AC ⊥ BD
AC = BD
Теорема.
Если диагонали прямоугольника пересекаются под прямым углом, то этот прямоугольник квадрат.
Доказательство.
Прямоугольник является параллелограммом, а параллелограмм, у которого диагонали пересекаются под прямым углом это ромб. То у ромба все стороны равны. Значит мы имеем прямоугольник у которого все стороны равны, а по определению это и есть квадрат. Теорема доказана.
Теорема.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство.
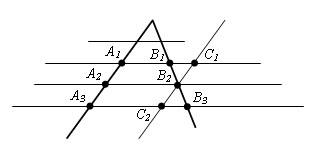
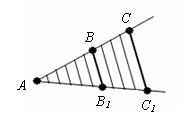
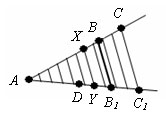
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.
Проведем через точку В2 прямую С1С2, параллельную прямой A1A2. Получаем параллелограммы A1C1BA2 и A2B2C2A3. По свойствам параллелограмма, A1A2 = C1B2 и A2A3 = B2C2. Так как A1A2 = A2A3, то C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3 по второму признаку равенства треугольников (C1B2 = B2C2, ∠ C1B2B1 = ∠ C2B2B3, как вертикальные, ∠ B1C1B2 = ∠ = B3C2B2, как внутренние накрест лежащие при прямых B1C1 и C2B3 и секущей С1С2). Из равенства треугольников следует, что B1B2=B2B3. Теорема доказана.
Средней линией треугольника называется отрезок, соединяющий средины двух его сторон.
Теорема.
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Доказательство.
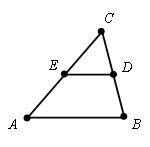
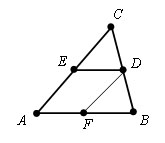
Пусть дан Δ ABC и его средняя линия ED.
Проведем прямую параллельную стороне AB через точку D. По теореме Фалеса она пересекает отрезок AC в его середине, т.е. совпадает с DE. Значит, средняя линия параллельна AB.
Проведем теперь среднюю линию DF. Она параллельна стороне AC. Четырехугольник AEDF – параллелограмм. По свойству параллелограмма ED=AF, а так как AF=FB по теореме Фалеса, то ED = ? AB. Теорема доказана.
|
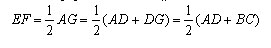
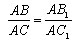
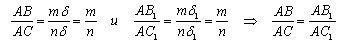
Комментариев нет:
Отправить комментарий