Треугольник и его свойства.

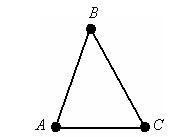
Треугольник Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки попарно. Точки называются вершинами, а отрезки – сторонами треугольника.    A, B и С – вершины треугольника. AB, BC и CA - стороны треугольника.  Треугольник обозначается указанием его вершин: треугольник ABC.  Вместо слова треугольник употребляется символ Δ. т.е. Δ ABC.  Углом треугольника ABC при вершине A (или углом между сторонами AB и AC) называется угол, образованный лучами AB и AC; ∠A = ∠BAC = ∠CAB. 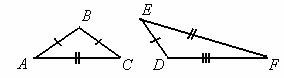Виды треугольников   Треугольник называется разносторонним, если любые две стороны его не равны друг другу. Δ ABC и Δ DEF разносторонни треугольники.    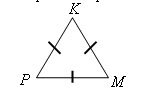Треугольник, все стороны которого равны, называется равносторонним. Δ PKM – равносторонний треугольник.  На сторонах треугольника ставят черточки, чтобы графически показать равные и различные по длине стороны треугольника. Если число черточек на сторонах треугольника совпадает, то эти стороны равны. PK=PM=KM.    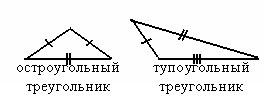Треугольник называется остроугольным, если все его углы острые. Треугольник называется тупоугольным, если один из его углов тупой. 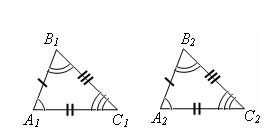Равенство треугольников   Два треугольника называются равными (Δ A1B1C1 = Δ A2B2C2), если у них соответствующие стороны равны и соответствующие углы равны. A1B1=A2B2, B1C1=B2C2, C1A1=C2A2 и ∠ B1A1C1 = ∠ B2A2C2, ∠ A1B1C1 = ∠ A2B2C2, ∠ B1C1A1 = ∠ B2C2A2.  Равные углы обычно графически отмечают одной, двумя или тремя дужками.  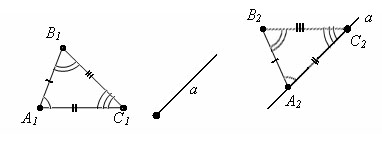Аксиома  Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.  Высота треугольника Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины, к прямой, которая содержит противолежащую сторону треугольника.    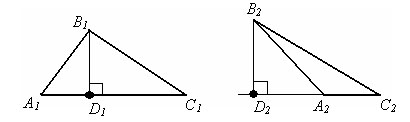B1D1 – высота треугольника A1B1C1, опущенная из вершины B1. B2D2 – высота треугольника A2B2C2, опущенная из вершины B2.  Биссектриса треугольника Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой противолежащей стороны.    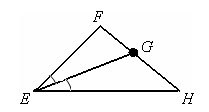EG – биссектриса угла FEH. ∠ FEG = ∠ GEH.  Медиана треугольника Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противоположной стороны треугольника.    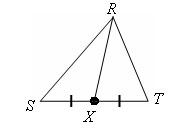RX – медиана угла SRT. SX = XT. 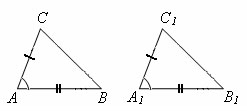Первый признак равенства треугольников Теорема    Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.  Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1. 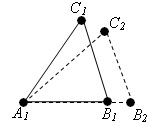  Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1.    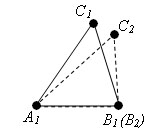Так как A1B1=A1B2, то вершины B1 и B2 совпадают.    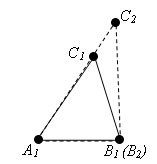Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2.    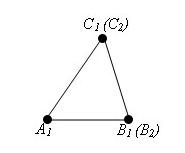Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана. Признак параллельности прямых Теорема.    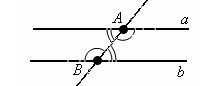Если внутренние накрест лежащие углы равны, то прямые параллельны  Доказательство.  Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы.    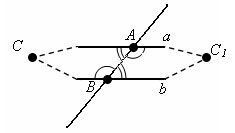Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке С.  Отложим от секущей AB треугольник ABC1, равный треугольнику ABC, так, что вершина С1 лежит в другой полуплоскости, чем вершина С.  По условию внутренние накрест лежащие углы при параллельных прямых a, b и секущей AB равны.  Из равенства треугольников следует, что ∠ CAB = ∠ C1BA и ∠ CBA = ∠ C1AB и они совпадают с внутренними накрест лежащими углами. Значит, прямая AC1 совпадает с прямой a, a прямая BC1 совпадает c прямой b. Отсюда следует, что через две различные точки С и С1 проходят две различны прямые a и b. Это противоречит аксиоме о том, что «Через любые две точки можно провести прямую, и только одну». Значит, прямые параллельны.  Из теоремы следует:  Две прямые, перпендикулярные третьей, параллельны.  На основании теоремы доказывается:  Если соответственные углы равны, то прямые параллельны.  Если сумма внутренних односторонних углов равна 180°, то прямые параллельны. 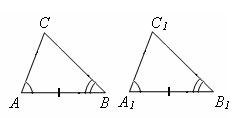Второй признак равенства треугольников Теорема    Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.  Доказательство.  Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, ∠ B = ∠ B1, AB = A1B1.    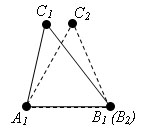Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана. Свойства параллельных прямых Теорема  Две прямые, параллельные третьей, параллельны.    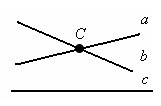Доказательство.  Пусть прямые a и b параллельны прямой с. Допустим, что прямые a и b не параллельны. Тогда они пересекаются в некоторой точке С. Получается, что через точку С проходит две прямые параллельные прямой с. Но это противоречит аксиоме «Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной». Теорема доказана.  Теорема  Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.    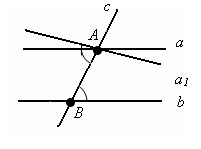Доказательство.  Пусть есть параллельные прямые a и b, которые пересекаются секущей прямой с. Прямая с пересекает прямую а в точке A и прямую b в точке B. Проведем чрез точку A прямую a1 так, что бы прямые a1 и b с секущей с образовали равные внутренние накрест лежащие углы. По признаку параллельности прямых прямые a1 и b параллельны. А так как через точку A можно провести только одну прямую параллельную b, то a и a1 совпадают.  Значит, внутренние накрест лежащие углы, образованные прямой a и b, равны. Теорема доказана.  На основании теоремы доказывается:  Если две параллельные прямые пересечены третьей прямой, то соответствующие углы равны.  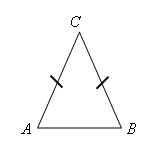Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180 º Равнобедренный треугольник   Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми (AC и CB), а третья сторона называется основанием (AB). Свойства углов равнобедренного треугольника Теорема  В равнобедренном треугольнике углы при основании равны.  Доказательство.  Пусть ABC – равнобедренный треугольник с основанием AB.    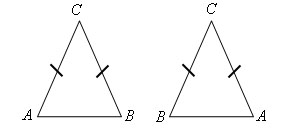Треугольник ACB равен треугольнику BCA по первому признаку равенства треугольников. AC = BC, CB = CA, ∠ C = ∠ C. Следовательно ∠ A = ∠ B. Теорема доказана. Признак равнобедренного треугольника Теорема  Если в треугольнике два угла равны, то он равнобедренный.    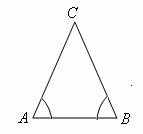Доказательство.  Пусть треугольник ABC такой, что ∠ A = ∠ B. Докажем что он равнобедренный.    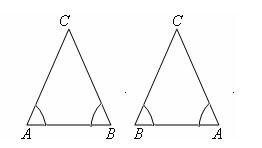Треугольник ACB равен треугольнику BCA, по второму признаку равенства треугольников, так как AB = BA, ∠ A = ∠ B, ∠ B = ∠ A. Следовательно, AC = BC. Получаем, что треугольник ABC равнобедренный. Теорема доказана. Свойство медианы равнобедренного треугольника Теорема  В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.    Доказательство.  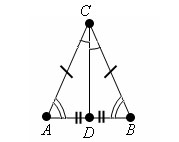Пусть ABC – равнобедренный треугольник, а CD медиана, проведенная к основанию AB этого треугольника.  Треугольники ACD и BCD равны по первому признаку равенства треугольников, так как AC=AB – так как ABC равнобедренный, AD=DB – так как CD медиана и разбивает основание AB пополам, ∠ CAD = ∠ CBD – так как ABC равнобедренный.  Из равенства треугольников следует:  1) так как ∠ ACD = ∠ BCD, то CD – биссектриса;  2) так как ∠ CDA = ∠ CDB и эти углы смежные, то они по 90 ° и CD – высота.  Теорема доказана. Свойство медианы и высоты равнобедренного треугольника Теорема  Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.    Доказательство.  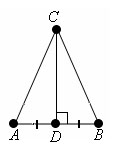Пусть в треугольнике ABC CD медиана и высота.  Тогда треугольники ACD и BCD равны по первому признаку равенства треугольников, так как CD общая для этих треугольников, AD=DB – так как CD медиана и разбивает AB пополам, ∠ CDA = ∠ CDB – так как CD высота.  Отсюда следует, что AC = CB и ABC – равнобедренный треугольник. Теорема доказана. Третий признак равенства треугольников Теорема  Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.    Доказательство.  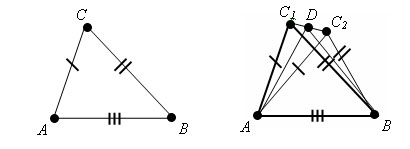Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны.  Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку.  Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1.  Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.