Движение в пространствее
Движением в пространстве называется преобразование, при котором сохраняется расстояния между точками.
Движение в пространстве обладает теми же свойствами, что и в плоскости и еще одним новым: движение переводит плоскости в плоскости.
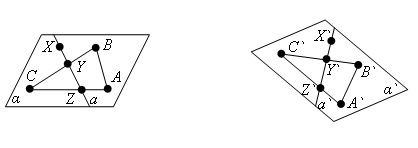
Доказательство
Пусть α - произвольная плоскость. Возьмем на ней три произвольные точки A, B и С, не лежащие на одной прямой. При движении они перейдут в A`, B`, C`, так же не лежащие на одной прямой. Проведем через них плоскоcть α`.
Докажем, что при таком движении плоскость α переходит в плоскость α`.
Пусть X – произвольная точка плоскости α. Проведем через нее какую-нибудь прямую a в плоскости α, пересекающую треугольник ABC в двух точках Y и Z прямой a перейдут в точки Y` и Z`, принадлежащие треугольнику A`B`C`, а значит, плоскости α`.
Значит, прямая a` лежит в плоскости α`. Точка X при движении переходит в точку X` прямой a`, а значит, и плоскости α`, что и требовалось доказать.
В пространстве две фигуры называются равными, если они совмещаются движением.
Параллельный перенос в пространстве
Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a, b, с одни и те же для всех точек (x; y; z).
Параллельный перенос в пространстве обладает следующими свойствами:
1. Параллельный перенос есть движение.
2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя.
4. Каковы бы ни были точки A и A`, существует единственный параллельный перенос, при котором точка A переходит в точку A`.
5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
Подобие пространственных фигур
Преобразование фигуры F называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же количество раз, т.е. для любых двух точек X и Y фигуры F и точек X`, Y` фигуры F`, в которые они переходят X`Y` = k * XY.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Гомотетия в пространстве
Теорема
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость ( или в себя при k=1).
Доказательство
Пусть, O – центр гомотетии и α - любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости α. Преобразование гомотетии переводит точку A в точку A` на луче OA, а точку B в точку B` на луче OB, причем
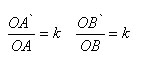
где k – коэффициент гомотетии. Отсюда следует подобие треугольников AOB и A`OB`. Из подобия треугольников следует равенство соответствующих углов AOB и A`OB, а значит, параллельность прямых AB и A`B`.
Возьмем теперь другую прямую AC в плоскости α. Она при гомотетии перейдет в параллельную прямую A`C`. При рассматриваемой гомотетии плоскость α перейдет в плоскость α`, проходящую через прямые A`B`, A`C`. Так как A`B` параллельна AB и A`C` параллельна AC, то по признаку параллельности плоскостей плоскости α и α` параллельны. Теорема доказана
Угол между скрещивающимися прямыми
Две пересекающиеся прямые образуют смежные и вертикальные углы. Вертикальные углы равны, а смежные углы дополняют друг друга до 180º. Угловая мера меньшего из них называется углом между прямыми.
Углом между скрещивающимися прямыми называется угол межу пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
Угол между прямой и плоскостью
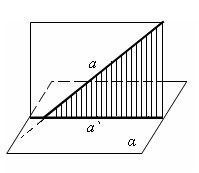
Прямая a пересекает плоскость α. а не перпендикулярна плоскости. Основания перпендикуляров, опущенных из точек прямой a на плоскость α, лежат на прямой a`. Эта прямая называется проекцией прямой a на плоскость α.
Угол между прямой и проекцией этой прямой на плоскость называется углом между прямой и плоскостью.
Угол между плоскостями
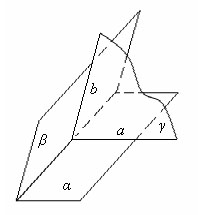
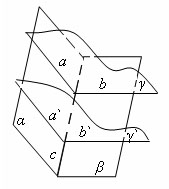
Пусть плоскости α и β пересекаются. Проведем плоскость γ, перпендикулярную прямой их пересечения. Эта плоскость пересекает плоскости α и β по двум прямым a и b. Угол между прямыми a и b и есть угол между данными плоскостями.
Угол между плоскостями. Свойство
Теорема
Угол между плоскостями не зависит от выбора секущей плоскости.
Доказательство.
Пусть есть две плоскости α и β, которые пересекаются по прямой с. проведем плоскость γ перпендикулярно прямой с. Тогда плоскость γ пересечет плоскости α и β по прямым a и b соответственно. Угол между плоскостями α и β равен углу между прямыми a и b.
Возьмем другую секущую плоскость γ`, перпендикулярную с. Тогда плоскость γ` пересечет плоскости α и β по прямым a` и b` соответственно.
При параллельном переносе точка пересечения плоскости γ с прямой с перейдет в точку пересечения плоскости γ` с прямой с. при этом по свойству параллельного переноса прямая a перейдет в прямую a`, b – в прямую b`. следовательно углы между прямыми a и b, a` и b` равны. Теорема доказана.
Площадь ортогональной проекции многоугольника
Теорема
Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.
Доказательство.
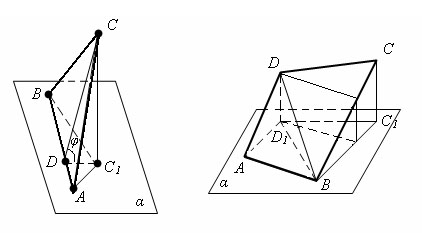
Пусть есть треугольник ABC и его проекция ABC1 на плоскость α. Проведем высоту CD треугольника ABC. По теореме о трех перпендикулярах отрезок C1D – высота треугольника ABC1. Угол CDC1 равен углу φ между плоскостью треугольника ABC и плоскостью проекции α.
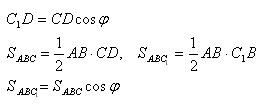
Следовательно, для треугольника теорема верна.
Пусть теперь есть многоугольник ABCD. Разобьем его на треугольники. Каждый треугольник, у которого нет стороны, параллельной плоскости проекции, разобьем на два треугольника с общей стороной, параллельной плоскости проекции. Получаем что для каждого треугольника Δ и его проекции Δ` в плоскости α верно равенство
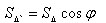
Сложим все эти равенства почленно. Получим
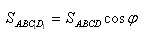
Теорема доказана.
Векторы в пространстве
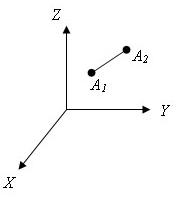
Вектором в пространстве называется направленный отрезок.
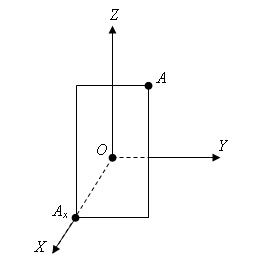
Координатами вектора с началом в точке A1(x1; y1; z1) и концом в точке A2(x2; y2; z2) называются числа x2-x1, y2-y1, z2-z1. Вектор обозначается в пространстве так:
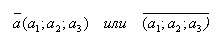
Действия над векторами
Суммой векторов a(a1; a2; a3) и b(b1; b2; b3) называется вектор c (a1+b1; a2+b2; a3+b3).
Произведение вектора a(a1; a2; a3) на число λ называется вектор λ a = (λa1; λa2; λa3).
Скалярным произведением векторов (a1; a2; a3) и (b1; b2; b3) называется число a1b1 + a2b2 + a3b3. |
|
|
|
|
|
|
|
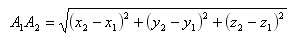
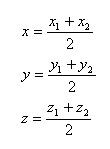

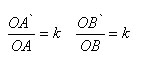




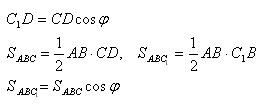
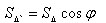
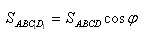
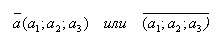
Комментариев нет:
Отправить комментарий