Основными геометрическими фигурами на плоскости являются точка и прямая.
Точки обозначаются прописными латинскими буквами: A, B, C,... .
Прямые обозначаются строчными латинскими буквами a, b, c,... .
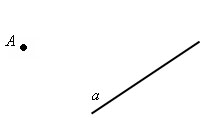
Прямая бесконечна. На рисунке изображается только ее часть, но мы представляем ее себе неограниченно продолженной в обе стороны.
Аксиома 1
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Аксиома 2 Через любые две точки можно провести прямую, и только одну.
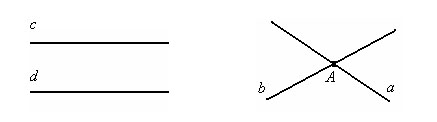
Если две прямые имеют общую точку, то говорят что они пересекаются.
Если две прямые не имеют общих точек, то говорят что они не пересекаются.
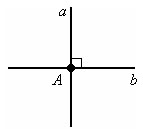
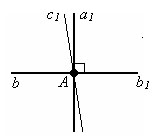
Прямая a пресекает прямую b в точке A. A – точка пересечения прямых a и b.
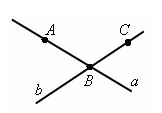
Точки A и B принадлежат прямой a. Тоска С не принадлежит прямой a.
Соответственно точки С и B принадлежат прямой b. Тоска A не принадлежит прямой b.
Так же говорят точки A и B лежат на прямой a, а точка С не лежит.
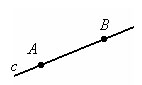
Прямую можно обозначить двумя точками лежащими на ней. Прямую с можно обозначить AB.
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками, которые называются концами отрезка.
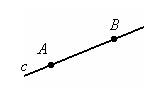
Точки прямой a, расположенные между точками A и B называются «отрезком AB». A и B – концы отрезка AB.
Аксиома 3 Из трех точек на прямой одна и только одна лежит между двумя другими.
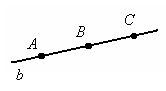
На прямой b три точки A, B и С. Точка В лежит между точками A и С или можно сказать, что точка В разделяет точки A и С. Иначе говоря, А и С лежат по разные стороны от точки B.
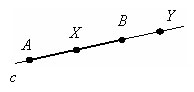
На прямой с точка X лежит между точками A и B, можно сказать X принадлежит отрезку AB. Точка Y не лежит между точками A и B, поэтому она не принадлежит отрезку AB.
Аксиома 4
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
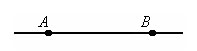
Расстоянием между двумя точками A и B называется длина отрезка AB.
При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
Два отрезка называются равными, если равны их длины.
Если взять на отрезке AB точку, пусть это будет точка С. То длина отрезка AB равна сумме длин отрезков AC и CB. Это можно записать так AB = AC + CB
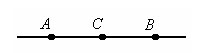
Обычно слово отрезок не пишут, а записывают название концов отрезков заключенными в квадратные скобки. Т.е. можно записать «отрезок AB» или [AB].
|
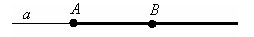



Комментариев нет:
Отправить комментарий