Решение треугольников.

Теорема косинусов

Теорема 

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. 

 

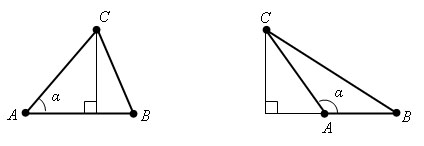
Доказательство. 

Пусть есть Δ ABC. 
Докажем, что 

 

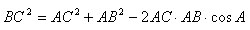
Имеем векторное равенство 

 

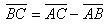
Возведем в квадрат левую и правую часть равенства, получим 

 

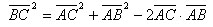
Или 

 

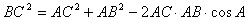
Теорема доказана.

Теорема синусов

Теорема 

Стороны треугольника пропорциональны синусам противолежащих углов. 

 

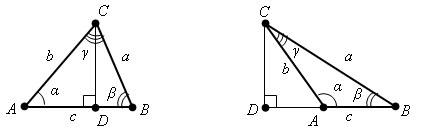
Доказательство. 

Пусть есть Δ ABC со сторонами a, b, с и углами α, β, γ. 
Докажем, что 

 

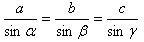
Проведем из точки С высоту CD. Тогда из Δ ACD получим: 

 

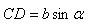
Если угол α тупой, то 

 

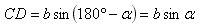
Из Δ BCD получаем 

 

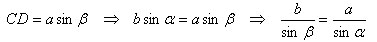
Аналогично получаем 

 

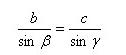
Теорема доказана.