Выпуклые многоугольники. Свойство
Теорема.
Сумма углов выпуклого n-угольника равна 180°*(n-2).
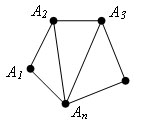
Доказательство.
Нужно заметить, n ≥ 3.
Для n = 3 многоугольник превращается в треугольник и теорема справедлива.
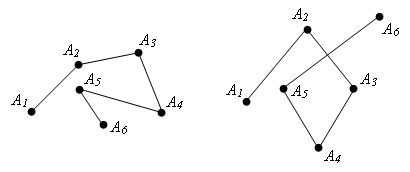
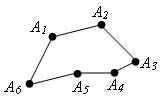
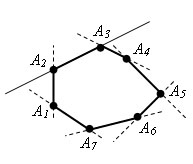
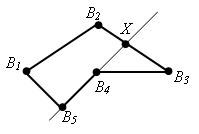
Для n > 3 проведем n-3 диагонали: A2An, A3An, …, An-1An. Получим n-2 треугольника: Δ A1A2An, Δ A2A3An, …, An-2An-1An. Сумма углов всех треугольников равна сумме углов многоугольника. Так как сумма углов треугольнике равна 180 ° и число треугольников равно n – 2, то сумма всех углов многоугольника равна 180° * (n - 2). Теорема доказана.
Правильные многоугольники
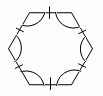
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
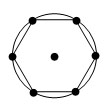
Если все вершины многоугольника лежат на некоторой окружности, то многоугольник называется вписанным в окружность.
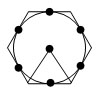
Если все стороны многоугольника касаются некоторой окружности, то многоугольник называется описанным около окружности.
Описанная и вписанная окружности правильного многоугольника имеют один и тот же центр, который называется центром многоугольника. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Формула для радиусов вписанных окружностей правильных многоугольников
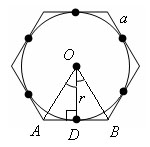
Теорема.
Сторона a правильного n-угольника связана с радиусом r вписанной окружности формулой
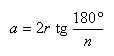
Доказательство.
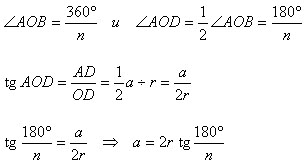
Теорема доказана.
Формула для радиусов описанных окружностей правильных многоугольниковв
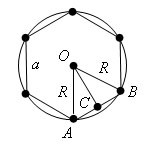
Теорема.
Сторона a правильного n-угольника связана с радиусом R описанной окружности формулой
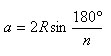
Доказательство.
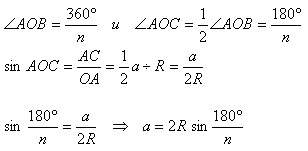
Теорема доказана.
Длина окружности
При неограниченном увеличении сторон правильного многоугольника его периметр приближается к периметру окружности.
Теорема
Отношение длины окружности к ее радиусу не зависит от окружности.
Доказательство.
Возьмем две произвольные окружности с радиусами R1 и R2 и длинами l1 и l2. предположим, что
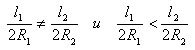
Впишем в окружности правильные n-угольники. N настолько велико, что периметры p1 и p2 правильных многоугольников приближаются к длинам окружностей l1 и l2. Поэтому заменим длины окружностей на периметры, тогда
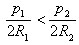
Но периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей:
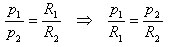
Что противоречит предположению. Теорема доказана.
Отношение длины окружности к диаметру обозначается греческой буквой π.
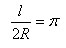
Радианная мера угла
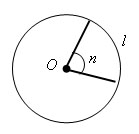
Пусть есть центральный угол n°. Развернутому углу соответствует длина полуокружности πR. Значит, углу в 1° соответствует дуга длины πR / 180, а углу в n° соответствует дуга длины.
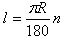
Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности. Следовательно,
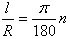
Из это видно, что радианная мера угла получается из градусной умножением на π/180°. |
|
|
|
|
|





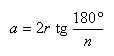
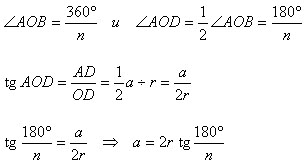

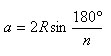
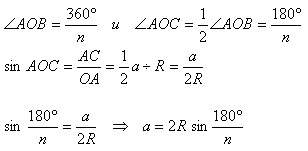

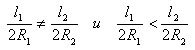
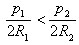
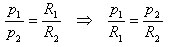
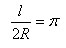

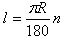
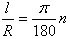
Комментариев нет:
Отправить комментарий