Основы стереометрии.

Стереометрия

Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. 

 

Плоскость обозначается греческими буквами α, β, γ, … .

Аксиомы стереометрии Система аксиом стереометрии состоит из аксиом планиметрии и 3 следующих:  1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.  2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.  3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну. Плоскость и точка Теорема  Через прямую и не лежащую на ней точку можно провести плоскость, и при том только одну.    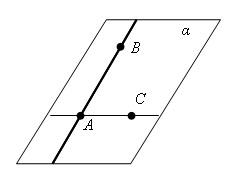Доказательство  Пусть AB – данная прямая и С – не лежащая на ней точка. Проведем через точки A и С прямую. Прямые AB и AC различны, так как точка С не лежит на прямой AB. Проведем через прямые AB и AC плоскость α. Она проходит через прямую AB и точку С.  Докажем, что плоскость α, проходящая через прямую AB и точку С, единственна.  Допустим, существует другая, плоскость α.`, проходящая через прямую AB и точку С. По аксиоме о том, что если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку, плоскости α и α` пересекаются по прямой. Эта прямая должна содержать точки A, B, C. Но они не лежат на одной прямой. Что противоречит предположению. Теорема доказана. Плоскость и прямая Теорема  Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.    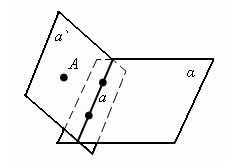Доказательство  Пусть a – данная прямая и α - данная плоскость. По аксиоме планиметрии 1 существует точка A, не лежащая на прямой a. Проведем через прямую a и точку A плоскость α`. Если плоскость α` совпадает с α, то плоскость α содержит прямую a, что и утверждается теоремой. Если плоскость α` отлична от α, то эти плоскости пересекаются по прямой a`, содержащей две точки прямой a.