Площади фигур.

Площадь   Фигура называется простой, если ее можно разбить на конечное число плоских треугольников.  Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:  1. Равные фигуры имеют равные площади;  2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.  3. Площадь квадрата со стороной, равной единице измерения, равна единице. 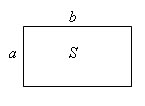Площадь прямоугольника   Площадь прямоугольника со сторонами a, b вычисляется по формуле S = a*b. Площадь параллелограмма   Теорема  Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a • h.  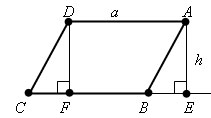Доказательство  Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то один из его углов A или B острый. Пусть для определенности A острый.  Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE • AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a • h. Теорема доказана. Площадь треугольника Теорема  Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a • h.      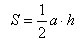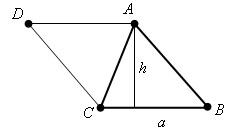Доказательство  Пусть ABC – данный треугольник. Дополним его до параллелограмма ABCD.  Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC. Высота параллелограмма, соответствующая стороне CB, равна высоте треугольника, проведенной к стороне CB. 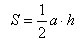Отсюда следует утверждение теоремы, и    Теорема доказана. 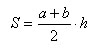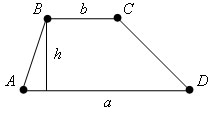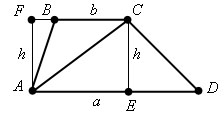Площадь трапеции   Теорема  Площадь трапеции равна произведению полусуммы его оснований на высоту    Доказательство    Пусть ABCD – данная трапеция  Диагональ AC трапеции разбивает ее на два треугольника: ABC и CDA. Следовательно, площадь трапеции равна сумме площадей этих треугольников. 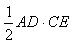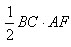Площадь треугольника ACD равна    Площадь треугольника ABC равна    Высоты AF и CE этих треугольников равны расстоянию h между параллельными прямыми BC и AD, т.е. высоте трапеции. 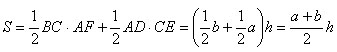Следовательно,    Теорема доказана. 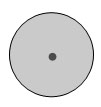Круг, круговой сегмент, круговой сектор   Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.    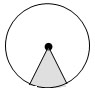Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла.    Круговым сегментом называется общая часть круга и полуплоскости. Площадь круга Теорема  Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.    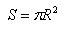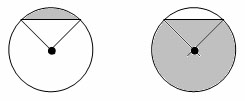Доказательство  Построим два правильных n-угольника: P1 – вписанный в круг и P2 – описанный около круга.    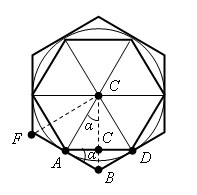Многоугольники P1 и P2 являются простыми фигурами. Многоугольник P2 содержит круг, а многоугольник P1 содержится в круге. Радиусы, проведенные в вершины многоугольника разбивают его на n треугольников, равных треугольнику AOD. 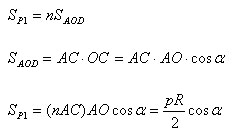Поэтому    где p – периметр многоугольника P1, R – радиус треугольника. 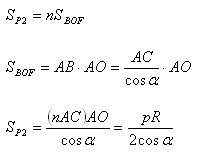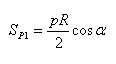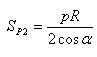Аналогично находим площадь многоугольника P2    Итак, многоугольник P1, содержащийся в круге, имеет площадь    И многоугольник P2, содержащий круг, имеет площадь    При достаточно большом n периметр p отличается сколь угодно мало от длины l окружности, а cos α сколь угодно мало отличается от единицы, поэтому площади многоугольников P1 и P2 сколь угодно мало отличаются от величины lR/2. 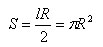Согласно определению площади произвольной фигуры это значит, что площадь круга    Теорема доказана. 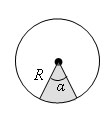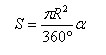Площадь кругового сектора   Площадь кругового сектора вычисляется по формуле    где R – радиус круга, а α - градусная мера соответствующего центрального угла. 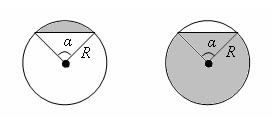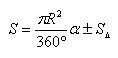Площадь кругового сегмента   Площадь кругового сегмента, не равного полукругу, вычисляется по формуле    где α - градусная мера соответствующего центрального угла, который содержит дугу этого кругового сегмента, а SΔ – площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак «-» надо брать, когда α < 180°, а знак «+» надо брать, когда α > 180°.