У нас есть две прямые x и y, которые пересекаются в точке O. Эти прямые называются осями координат. Ось x называется осью абсцисс, а ось y – осью ординат. Точка пересечения осей называется началом координат. Каждая ось разбивает плоскость на две полуплоскости, одна из них положительная, другая отрицательная.
Будем обозначать плоскость Oxy (O - точка пересечения оси x с осью y).
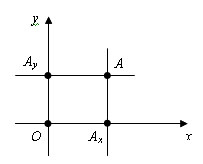
Любой точки плоскости, допустим точки A, можно сопоставить пару чисел, эта пара чисел называется координатами точки. Они определяются так:
1) проведем через точку A прямую, параллельную оси ординат. Эта прямая пересечет ось абсцисс x в некоторой точке Ax . Число x, абсолютная величина которого равна расстоянию от точки O до точки Ax , называется абсциссой точки A.
2) проведем через точку A прямую, параллельную оси абсцисс. Эта прямая пересечет ось ординат x в некоторой точке Ax. Число y, абсолютная величина которого равна расстоянию от точки O до точки Ay, называется ординатой точки A.
Если Ax принадлежит положительной полуоси, то это положительно число, если отрицательной – отрицательное число.
Если Ay принадлежит положительной полуоси, то это положительно число, если отрицательной – отрицательное число.
Если точка A лежит на оси ординат y, то x=0.
Если точка A лежит на оси абсцисс x, то y=0.
Координаты точки A записываются так: A (x; y).
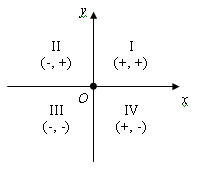
Плоскость разбивается координатными осями на четыре части – четверти: I, II, III и IV. В пределах одной четверти знаки обеих координат сохраняются и имеют значения, как на рисунке.
Введенные на плоскости координаты x и y называются декартовыми координатами.
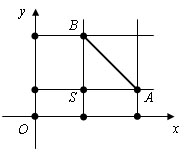
Даны две точки A (x1; y1) и B (x2; y2). Найдем расстояние между точками A и B.
Опустим перпендикуляры из точек A и B на ось абсцисс и на ось ординат. Как видно из рисунка, пара перпендикуляров пересекаются в точке S. Расстояние между точками B и S равно |y1-y2|, а расстояние между точками S и A равно |x1-x2|. Получаем треугольник SBA. По теореме Пифагора
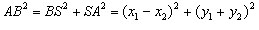
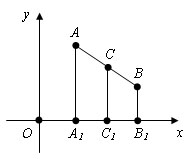
Пусть A(x1; y1) и B(x2; y2) – пусть две произвольные точки, а С(x; y) – середина отрезка AB. Проведем через точки A, B и С прямые параллельные оси y. Они перtсекут ось x в точках A1, B1 и С1. По теореме Фалеса точка С1 будет серединой отрезка A1B1. C1A1 = C1B1 и следовательно |x-x1|=|x-x2|. Отсюда следует, что либо x-x1=x-x2, либо x-x1=-(x-x2). Первое равенство невозможно, так как x1≠x2. Поэтому верно второе и следовательно
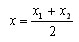
Так же получаем, что
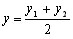
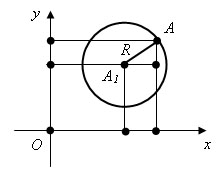
Пусть есть окружность с центром в точке A1 (a; b) и радиусом R. Возьмем произвольную точку A (x; y) на окружности. Тогда, как видно из рисунка, по теореме Пифагора
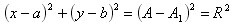
- это уравнение окружности.
Если центр окружности находится в начале координат, т.е. a=0 и b=0, то уравнение окружности принимает вид:
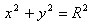
Обратно: любая точка A, координаты которой удовлетворяет данному уравнению окружности, принадлежат окружности.
Теорема
Уравнение вида ax + by + c = 0 при условии, что a и b одновременно не равны нулю, задает прямую в плоскости Oxy, и наоборот, уравнение произвольной прямой может быть записано в указанном виде.
Доказательство.
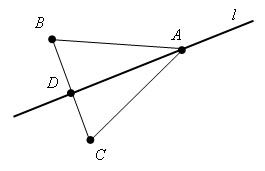
Пусть l – произвольная прямая в плоскости Oxy. Проведем какую-нибудь прямую перпендикулярно прямой l. Пусть они пересекаются в некоторой точке D. Отложим на перпендикулярной прямой точки B и C так чтобы BD=DC.
Пусть a1, b1 – координаты точки B и a2, b2 – координаты точки С. Как известно, любая точка A (x; y) прямой l равноудалена от точек B и С. Поэтому координаты точки A удовлетворяют уравнению
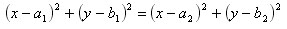
Верно и обратное: если координаты x и y какой-либо точки удовлетворяют данному уравнению, то эта точка равноудалена от точек B и C, а значит, принадлежит прямой l. Таким образом, уравнение является уравнением прямой l.
Раскроем скобки в этом уравнении и перенесем все ее члены в левую часть:
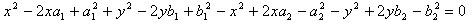
Сгруппируем члены так:
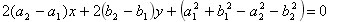
Обозначим
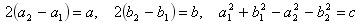
Получим
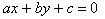
Теорема доказана.
Замечание.
Если a = b = 0, то уравнение ax + by + c = 0 имеет вид c = 0. При этом любая точка плоскости удовлетворяет исходному уравнению, а если a = b = 0, а c ? 0, то ни одна точка плоскости Oxy не удовлетворяет данному уравнению.
Пусть заданы уравнения двух прямых:
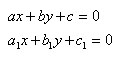
Найдем координаты их точки пересечения. Так как точка пересечения принадлежит обеим прямым, значит ее координаты удовлетворяют обоим уравнениям. Значит координаты точки пересечения являются решением системы уравнений, которые задают прямые. Значит нужно решить систему
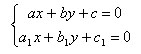
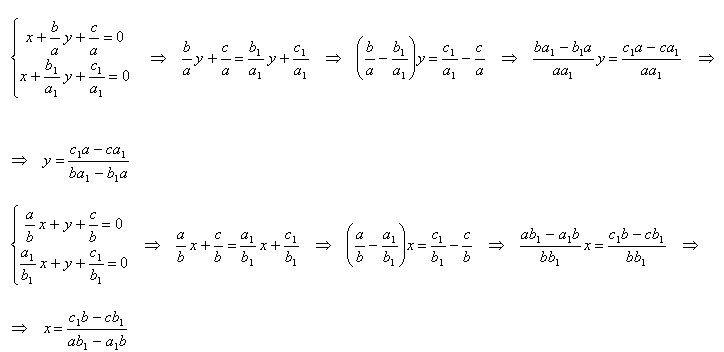
Точка с координатами
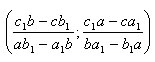
- точка пересечения заданных прямых.
Прямая имеет уравнение ax+by+c=0, рассмотрим частные случаи:
1) a = 0, b ≠ 0. Тогда уравнение прямой принимает вид:

.

Все точки прямой, вне зависимости от значения абсциссы x, имеют одну и ту же ординату

и прямая параллельная оси x. Если с=0, то прямая совпадает с осью x.
2) a , b = 0. Тогда уравнение прямой принимает вид:

.

. Все точки прямой, вне зависимости от значения ординаты y, имеют одну и ту же абсциссу

и прямая параллельная оси y. Если с=0, то прямая совпадает с осью y.
3) c = 0. Тогда прямая проходит через начало координат и его можно записать в виде:

.

Преобразуем уравнение прямой ax + by + c=0 к виду
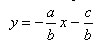
Введем обозначения
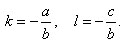
Тогда получим y = kx + l.
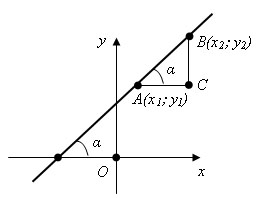
Возьмем две точки на прямой A (x1; y1) и B (x2; y2), такие что x1 < x2.
Их координаты удовлетворяют уравнению прямой:
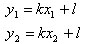
Вычитая эти равенства почленно, получим
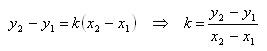
Проведя прямую через точку A параллельно оси x и прямую через точку B параллельную оси y, мы получим треугольник ABC. Замечаем, что
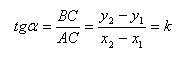
Если прямая расположена следующим образом :
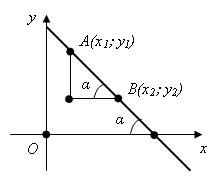
То
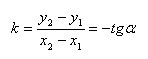
Таким образом, коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x.
Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.
Комментариев нет:
Отправить комментарий